
- •Кванттық механика лекция
- •1.1.Атомның тұрақтылығының және сәуле шығаруының мәселелері. Жарықтың корпускулалық қасиеттерінің байқалуы.
- •1.2.Комптон эффектісі
- •1.3 Атом энергиясының деңгейлерінің дискреттілігі. Бордың жартылай классикалық теориясы
- •1.4. Де Бройл гипотезасы. Корпускулалық толқындық дуализм
- •2.1 Күй функциясы. Күйлердің суперпазитция принципі.
- •2.2.Шредингер теңдеуінің түрі және оның шешімінің жалпы қасиеттері. Стационар күйлер.
- •2.3. Ықтималдық ағынының тығыздығы.
- •2.4.Бөлшектер санының сақталу заңы. Бөлшектердің еркін қозғалысының толқындық функциясы.
- •3.1. Импульстің анықталмаған мәніндегі күйі.
- •3.2.Толқындық пакет.
- •3.3.Гейзенбергтің анықталмағандықтар арақатынасы.
- •3.4.Анықталмағандықтар арақатынасы және физикалық шамаларды өлшеу. Энергия мен импульс үшін анықталмағандықтар арақатнасы.
- •3.5. Энергиямен импульс үшін анықталмағандықтар арақатынасы.
- •4.1.Финитті және инфинитті қозғалыстар.
- •4.2.Бір өлшемді потенциалдық шұңқырдағы бөлшек.
- •4.3.Төрт бұрышты потенциалды бөгет. Түнелдік эффект
- •5.1 Есептің қойылуы. Гармоникалық осциллятор үшін Шредингер теңдеуін шешу.
- •5.2. Гармоникалық осциллятор есебінің шешімін талдау.
- •5.3.Квазиклассикалық жуықтаулар.
- •6.1.Функцияны жалпыланған қатарға жүктеу. Фурье интегралы.
- •6.2.Сызықты операторлар.
- •6.3.Меншікті функциялар және операторлардың меншікті мәндері.
- •6.4.Өздік түйіндес операторлар.
- •8.1 Физикалық шамалардың орташа мәндерінің уақыт өтуімен өзгеруі, Эренфест теңдеуі
- •9.3 Орталық симметриялық өрістегі бөлшектің қозғалысы.
5.3.Квазиклассикалық жуықтаулар.
Шредингер
теңдеуі нақты өрісте қозғалатын
бөлшектірдің аз ғана саны үшін аналитикалық
шешімі болады.Шредингер теңдеуінің
жуықтап шешудің бірнеше тәсілі дамыған:
микробөлшектің бір өлшемді қозғалатынын
қарастырғанда кванттық механикада
классикалық жуықтау әдісі немесе
Вентцель-Крамерс-Бриллюэн әдісі деп
аталатын әдіс кеңінен қолданылады.Ол
үшін бір өлшемді қозғалыс үшін Шредингер
теңдеуін жазайық.2-ші ретті дифференциялды
штрих арқылы белгілейік:
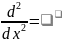
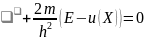 (14),
(14),
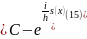 Мұндағы:c-тұрақты шама
Мұндағы:c-тұрақты шама
S(x)-әсердің өлшемімен өлшенетін белгісіз функция (15)-ші теңдеуді (14)-теңдеуге қойсақ
( (1
(1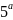 ),
Классикалық импульс модулі үшін
өрнектен:
),
Классикалық импульс модулі үшін
өрнектен: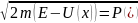
Олай
болса,(15)-ші теңдеу мына түрге келеді:
(16) Осы өрнекті жуықтап шешудің
арқасында:
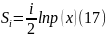 Осыны ескеріп,(15)-ші өрнекті былайша
жазамыз
Осыны ескеріп,(15)-ші өрнекті былайша
жазамыз
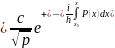 (18).
(18).
6.1.Функцияны жалпыланған қатарға жүктеу. Фурье интегралы.
Кванттық механикадағы суперпозиция принципі функцияны қатарға жіктеумен немесе Фурье интегралымен тығыз байланысты. Функцияны қатарға жіктеудің математикалық негіздерін еске түсірейік.
φ
= φ (к,х) функциясы берілсін. к- дискретті
түрде өзгеретін шама болсын. х-кеңістіктегі
нүктенің 3 координатының жиынтығы. Егер
к белгілі бір ретпен нөмірленсе онда
функция былайда жазады.
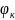 =φ(х)
к=1,2,3…
(х)
функциялар жүйесі бірге нөмірленген
және жұп-жұбымен ортогональды болса
ортонормальданған функциялар деп
аталады. Ортонормалдану шарты келесі
қатынаспен анықталады.
=φ(х)
к=1,2,3…
(х)
функциялар жүйесі бірге нөмірленген
және жұп-жұбымен ортогональды болса
ортонормальданған функциялар деп
аталады. Ортонормалдану шарты келесі
қатынаспен анықталады.
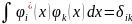 (1)
Мұндағы
(1)
Мұндағы
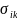 -
Кронекер символы деп аталады. Егер i мен
k бір-біріне тең болмаса онда
=0.
i≠k ,
=0
, i=k ,
=1,
-
Кронекер символы деп аталады. Егер i мен
k бір-біріне тең болмаса онда
=0.
i≠k ,
=0
, i=k ,
=1,
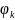 (x)
жүйесі толық деп аталады , егер барлық
функциялар жүйесіне ортогоналды және
жүйеге енбейтін функциялар болмаса.
(x)
жүйесі толық деп аталады , егер барлық
функциялар жүйесіне ортогоналды және
жүйеге енбейтін функциялар болмаса.
6.2.Сызықты операторлар.
Оператор- басқа функция алу үшін берілген қандай да бір функцияның үстінен орындалатын әрекет немесе әрекеттер бағдарламасын белгілеу үшін енгізілген символды айтады. Операторды әдетте латын алфавитінің бас әрпімен (қалпағы бар) белгілейді. Мысалы : Â- операторы. Егер оператор қандай да бір функцияның сол жағында тұрса онда бұл оператор функцияға әсер етеді деп атайды. Оператордың функцияға әсерінен айнымалылары алғашқы функцияның айнымалыларымен сай келетін жаңа функция пайда болады. Âψ= φ (1) , Оператор немесе оператордағы әрекеттер бағдарламасы математикалық символдармен немесе сөздермен бейнеленеді.
Мысалы: 1) Â=xx-айнымалыларына көбейту операторы.
2)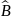 =
= x-бойынша
дифференциалдау операторы.
x-бойынша
дифференциалдау операторы.
3)
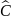 -
комплекс түйіндес оператор
-
комплекс түйіндес оператор
Сонымен,
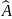 φ=xφ
;
φ=xφ
;
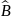 ψ=
ψ=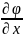 ;
;
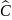 φ=
φ=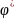 ;
Оператор сызықты деп аталады , егер
келесі шарт орындалса .
;
Оператор сызықты деп аталады , егер
келесі шарт орындалса .
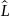 (
( +
+ )=
)=
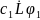 +
+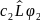 (2)
(2)
 ,
,
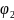 -
қандай
да бір функциялар,
-
қандай
да бір функциялар,
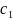 ,
,
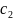 -
тұрақты ( комплексті) сандар
-
тұрақты ( комплексті) сандар
Мысалы: дифференциалдау операторы және көбейту операторы сызықты операторға жатады. Екінші өрнектегі шартқа сай тұрақты көбейткіштерде сызықтық оператордың алдына шығарып жіберуге немесе көбейтіп жіберуге болады. Кванттық механикада сызықтық оператор қолданылады. Оператор символы дербес математикалық нысан ретінде қарастырылады және олардың үстінен кейбір математикалық амалдар қолданылады, атап айтқанда қосу , көбейту, дәрежеге шығару, қатарға жіктеу тағы басқа.
Оператор қасиетін қарастырайық.
Операторды қосу және көбейту.
операторы Â және қосындысы деп аталады, егер келесі шарт орындалса.
φ = Âφ + φ (3), Анықтамадан: φ= (Â+ )φ (3*)
Операторды қосу ережесі ассоциативті және комутативті қасиеттерге ие. Яғни (Â+ )+ = Â+ ( + ) ассоциативті, Â+ = +Â –комутативті
операторы Â және операторының көбейтіндісі деп аталады, егер келесі шарт орындалса.
 =
=
 (
φ)
(4), Анықтамаға сай
=Â
(
φ)
(4), Анықтамаға сай
=Â
Көбейту операторы комутативті емес деп аталады , егер Â ≠ Â(5)
Көбейту операторы жалпы жағдайда комутативті емес, егер Â = Â шартты қанағаттандырса. Ондай оператор комутативті оператор деп аталады.
Сонда:
