Кванттық механика лекция

1.1.Атомның тұрақтылығының және сәуле шығаруының мәселелері. Жарықтың корпускулалық қасиеттерінің байқалуы.

ХХғасырдың басында атомның планетарлық моделі жасалды. Бұл модель бойынша атом – центрінде оң зарядталған ядродан және оны шыр көбелек айналатын электрондар бұлытыдан тұратын бейтарап жүйе Ядро өз кезегінде протондар мен нейтрондардан тұрады. Сүтегі ядро электронның массасынан шамамен 2000 есе ауыр және электронды ядро өзіне кулон күшімен тартып ұстап тұрады. Олай болса , сүтегі ядросының маңында айналған электрон үшін қозғалыс теңдеуін жазайық: ma=F a=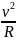 F=k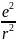 Орнына қойсақ , m 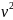= k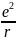 (1) Электронның ядро маңындағы қозғалысы үдемелі. Олай болса макроскопиялық электродинамиканың теориясы бойынша, кез – келген үдемелі қозғалған зарядтың өзінен электромагниттік сәуле шығаратыны белгілі. Ол сәулелену қуатының өрнегіне 1 ші өрнекті пайдалансақ , N = 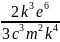(2) . Бұл қуат шамамен 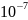Дж/с қуатқа тең. Ал электронның энергиясы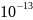 Дж дан аспауы тиіс. Олай болса электрон 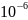сек тан кейін атомға құлап , атом жойылып кетуі тиіс. Шындығында атом орнықты жұйе яғни тұрақты. Осылайша эксперимент пен теория арасында қарама – қарсылық туындады яғни атомның орнықтылығын классикалық механика зарядтары түсіндіре алмайды. Сонымен атом қозбаған күйде өзінен электромагниттік сәуле шығармайды , тек атом бір қозған күйден екінші күйге көшкенде ғана өзінен сәуле шығарады. Классикалық механика заңдарына сәйкес , электронның жылдамдығы өзгеру салдарынан тұтас спектрлер пайда болу қажет ХІХ ғасырдың ІІ жартысында спектроскопияның дамуымен сызықтық спектр шығаратыны белгілі болды. Олай болса ,классикалық механика заңдары атомның сәуле шығаруын дұрыс түсіндіре алмады. Мысалы, тәжірибелік жолмен алынған сүтегі атомының спектрінің өрнегі υ =R (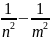 ) (3) Бұл өрнектіде классикалық механика және электродинамика заңдарымен түсіндіре алмады.

1.1.2.

Атомның планетарлық моделі пайда болғанға дейін-ақ ХІХ ғасырдың ІІ жартысында абсолют қара дененің сәуле шығаруы терең зерттеле бастады. Термодинамикалық тұрғыдан қарағанда абсолют қара дененің жылулық спектрі оның құрылымына тәуелді болмауы тиіс. Яғни, абсолют қара дененің қарапайым моделі ретінде нақты атомдар мен молекулалар электромагниттік толқынды шығару және жұту қабілетіне ие гармоникалық осцилятормен алмастырылды.Осылайша жүргізілген есептеулер эксперименттік мәліметтермен сәйкес келмеді . Яғни , классикалық теория абсолют қара дененің сәуле шығаруын түсіндіре алмады. Бұл қиыншылықтар 1900 жылы Макс Планк ұсынған атомдық жүйенің энергиясының дискреттік деңгейлері туралы гипотезасы алып шықты. E = n hυ n = 0,1,2,3…..ал υ – осцилятордың жиілігі, h = 6,62 * 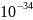Дж/с Бұл Планк тұрақтысы деген атқа ие болды.Планктың идеясын Эйнштейн жетілдіре отырып 1907 жылы қатты денелердің жылу сыйымдылығының температураға тәуелділігін түсіндіре алды Эйнштейн идеясы бойынша орнын электромагниттік өріс элементар бөлшектер тұарды Бұл бөлшектердің ( фотонның энергиясымен импульсі келесі өрнектермен анықталады) E = ℏω, = ℏ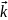 Мұндағы , ℏ = = 1.05 * Дж*с – толқындық вектор = = 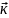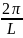ℏ - Планк тұрақтысы

Электромагниттік өрістің квантталуын негізге ала отырып, Эйнштейн фотоэффект теориясын жасады. hυ = +

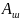Жарықтың корпускулалық табиғатын дәлелдейтін басқада эксперименттік еңбектер болды. Оның бірі 1923 жылы Комптон тәжірибесінің нәтижесінде алынған Комптон эффектісі деп аталатын атпен белгілі эксперимент.