5.3. Продолжительность охлаждения

В холодильной технологии пользуются обычно решениями для простого охлаждения тел при следующих условиях:

теплофизические свойства тела не меняются во время его охлаждения;

температура охлаждающей среды постоянна;

коэффициент теплоотдачи на поверхности тела постоянен;

действие каких-либо дополнительных источников или стоков тепла в теле, не включенных в его теплоемкость, не учитывается.

Расчет продолжительности охлаждения пищевых продуктов, когда не соблюдаются точно ни условия простого охлаждения пищевых продуктов, ни условия однородности охлаждаемого тела, ни простота формы, не может дать безукоризненных результатов. Обычное отклонение результатов такого расчета от опытных данных охлаждения пищевых продуктов составляет 10-15 %, но иногда может быть и большим.

Пусть t_с - постоянная температура охлаждающей среды, t_х - переменная температура в точке охлаждаемого тела, координата которой х. В начальный момент температура во всех точках тела одинакова и равна t_н.

Следовательно, при τ = 0, t_х = t_н

t_н – t_с = ; t_х – t_с = .

Введем безразмерные комплексы:

и ,

где ℓ - характерный линейный размер тела, составляющий половину толщины для плоской пластины, радиус для цилиндра и шара.

Для одномерного распространения тепла дифференциальные уравнения теплопроводности при граничных условиях третьего рода:

; .

Подставив в эти уравнения безразмерные комплексы, получим новую форму записи уравнений:

для уравнения теплопроводности:

или ,

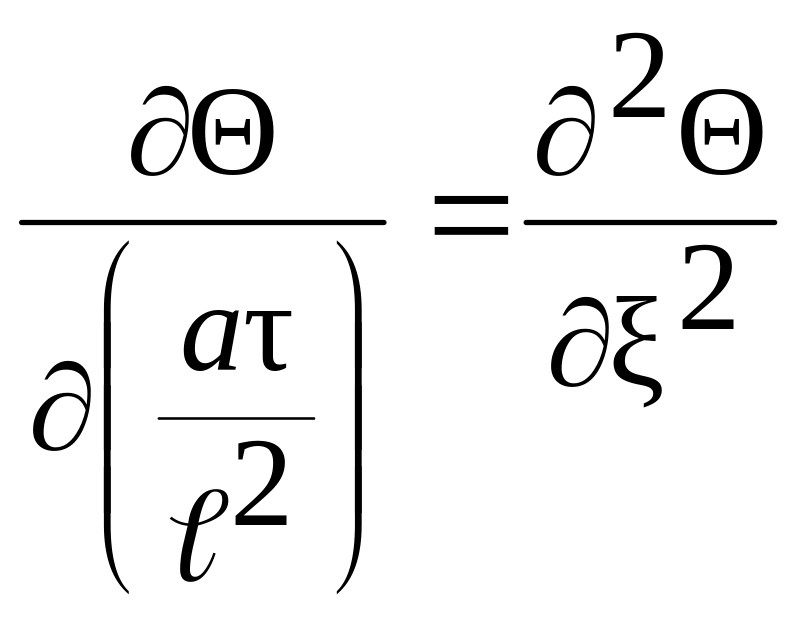где ;

следовательно, ;

после решения получаем следующее выражение:

или ,

где ,

следовательно, .

Обычно охлаждение пищевых продуктов осуществляется при отводе тепла конвекцией в воздухе или жидкости, и продолжительность процесса приходится определять применительно к граничным условиям третьего рода. Тогда описание теплообмена посредством обоих уравнений приведет к выражению:

.

Графики, которыми пользуются для числовых решений, даются отдельно для различных форм тела, центральной их части (плоскость-в пластине, ось-в цилиндре и центр-в шаре) и для поверхности тела (рис. 5.1, стр. 73-75).

В графиках дана связь между безразмерной избыточной температурой и критерием Био Bi для различных значений критерия Фурье Fо, представленных отдельными линиями в координатах Bi- . Те же решения даны в иных формах математической записи и сопровождаются таблицами числовых значений величин, нужных для вычисления.

Представленный способ вычисления продолжительности охлаждения позволяет найти время, нужное для достижения заданной температуры на поверхности или в центре тела, или температуру в тех же точках спустя заданное время от начала охлаждения, так как температура t входит в безразмерный комплекс , а время τ - в критерий Fо.

Для расчета продолжительности охлаждения пищевых продуктов А. Фикиин и И. Фикиина предложили пользоваться формулой, полученной из классического решения с некоторыми упрощениями задачи об охлаждении простых однородных тел:

,

где А_{ф -} эмпирический коэффициент, учитывающий форму продукта (А_ф = 1 для пластины, А_ф = 0,5 для цилиндра, А_ф = 1/3 для шара).

Продолжительность охлаждения можно рассчитать на основе закона регулярного теплового режима. В холодильной технологии этим методом пользуются особенно широко вследствие его простоты и универсальности.

Для холодильной технологии представляют интерес лишь некоторые стороны содержания и практических приложений этих исследований.

Рис. 5.1. Номограммы для определения продолжительности охлаждения:

а - на поверхности цилиндра; б - в середине пластины

Рис. 5.1. Номограммы для определения продолжительности охлаждения:

в - на поверхности неограниченной пластины; г - на оси цилиндра

Рис. 5.1. Номограммы для определения продолжительности охлаждения:

д - на поверхности шара; е - в центре шара

Первая стадия простого охлаждения или нагревания тела сильно зависит от его начального температурного поля; это иррегулярная стадия охлаждения или нагревания.

Вторая стадия независимо от начального температурного поля характеризуется экспоненциальным изменением температуры во всех точках тела, а также его среднеобъемной температуры во времени; эта стадия называется регулярным тепловым режимом.

Третья стадия, теоретически наступающая спустя лишь бесконечно длительное время от начала охлаждения, характеризуется достижением теплового равновесия, когда температура тела во всех точках становится равной температуре внешней охлаждающей или нагревающей среды.

Таким образом, регулярный тепловой режим наступает лишь спустя некоторое время после начала теплообмена, но затем длится неограниченный период времени. Продолжительность первой иррегулярной стадии процесса зависит от сочетания геометрических, теплофизических свойств тела, его начального температурного поля и условий охлаждения. В частных случаях она может быть представлена как функция критерия Био.

Из классического решения задачи о простом охлаждении или нагревании тел следует, что существуют условия, когда при достаточно большой величине критерия Фурье наступает регулярный тепловой режим.

Пусть при охлаждении в среде с неизменной температурой и постоянным коэффициентом теплоотдачи не меняются теплофизические свойства тела и можно пренебречь тепловыделениями и теплопоглощениями, не учитываемыми постоянной теплоемкостью тела.

Представим уравнение теплового баланса при охлаждении в виде равенства произведения массы G, теплоемкости с и изменения температуры dt, с одной стороны, и количества теплоты, отведенного от поверхности тела, с другой.

Обозначим комплекс величин αS/(Gс) = m. В этом случае из представленного уравнения теплового баланса при малых значениях критерия Био или без учета неравномерности температурного поля тела во время охлаждения скорость понижения температуры t в любой точке тела выражают законом Ньютона.

(5.2)

Переходя к переменной избыточной температуре , имеем:

или

. (5.3)

Интегрируя выражение (5.3) и принимая во внимание, что постоянная интегрирования из условия τ = 0 окажется начальной избыточной температурой , получим

. (5.4)

Из выражения (5.4) найдем продолжительность охлаждения в пределах действия закона, представленного формулой (5.2).

(5.5)

Отыскание величины m - темпа охлаждения - связано с проведением эксперимента. Пусть для моментов времени τ₁ и τ₂ формула (5.5) примет вид:

; (5.6)

. (5.7)

Вычтя из формулы (5.6) формулу (5.7), получим:

.

Тогда .

Представим графическую интерпретацию представленной выше формулы (рис. 5.2). Из графика видно, что m представляет собой тангенс угла наклона линии графика к оси времени.

Как видно из рис. 5.2, чем быстрее понижается температура тела, тем больше будет угол наклона α, а значит тем больше m. Параметр m назван темпом охлаждения, так как по его значению можно судить о скорости процесса.

Рис. 5.2. Зависимость логарифма избыточной температуры ln

от времени τ при регулярном режиме охлаждения

Для характеристики поля температур тела вводят также коэффициент неравномерности температурного поля ψ в виде отношения избыточной температуры поверхности тела к его среднеобъемной избыточной температуре:

.

В предельных случаях при α → ∞, _ст → 0 и → 0; при α → 0, _ст → _v и → 1.

Таким образом, коэффициент неравномерности температурного поля тела представляет собой положительную правильную дробь. Он остается постоянным, когда охлаждение или нагревание любого данного тела совершается по закону регулярного теплового режима.

С учетом коэффициента неравномерности температурного поля общее выражение темпа охлаждения следующее:

. (5.8)

При α = 0 темп охлаждения обращается в нуль, а это соответствует прекращению охлаждения, что совершенно логично.

Формула (5.8) выражает темп охлаждения как величину, пропорциональную отношению площади поверхности тела к его обшей теплоемкости с множителем в виде произведения ψα, превращающегося в неопределенность при α = ∞. Но по физическому смыслу явлений условие α = ∞ означает, что температура поверхности постоянна на протяжении всего охлаждения и равна температуре внешней среды, а это сводит теплообменный процесс к граничным условиям первого рода. Тогда темп охлаждения при α=∞, обозначаемый m, будет, очевидно, зависеть от температуропроводности тела а и его геометрической характеристики К_ф, связывающей форму и размеры.

, (5.9)

где К_ф - коэффициент формы;

для шара радиусом R

К_ф = (R/π)²;

для цилиндра радиусом R и длиной h

;

для прямоугольного параллелепипеда со сторонами

.

Темп охлаждения m есть конечная, положительная величина, постоянная для тела данных размеров и формы при данной величине коэффициента его температуропроводности.

Таким выражением для определения продолжительности охлаждения часто пользуются в холодильной технологии; применимость его неоднократно подтверждена даже в случаях охлаждения плодов и мяса в воздухе, хотя при этом происходят внутренние тепловыделения и отвод теплоты испарением. При расчетах по выражению (5.5) (см. стр. 77) множитель m берут по данным опыта. Постепенное убывание внутренних тепловыделений продуктов и одновременное сокращение отвода теплоты испарением взаимно компенсируются.