3.3. Главные площадки и главные напряжения. Инварианты напряженного состояния

Будем полагать, что среди бесконечного множества площадок в окрестности исследуемой точки существуют площадки, свободные от касательных напряжений. Такие площадки называют главными. Нормальные напряжения на главных площадках также называются главными.

Пусть – внешняя нормаль к главной площадке, а – направляющие косинусы этой нормали. Для главной площадки полное напряжение . Проецируя полное напряжение на координатные направления, с учетом (3.4) получим:

(3.8)

Преобразуя (3.8), придем к системе однородных уравнений:

(3.9)

С учетом

(3.9’)

тривиальное решение невозможно. Следовательно, определитель, составленный из коэффициентов системы (3.9), должен равняться нулю:

. (3.10)

Раскрывая определитель, получим кубическое уравнение

(3.11)

где 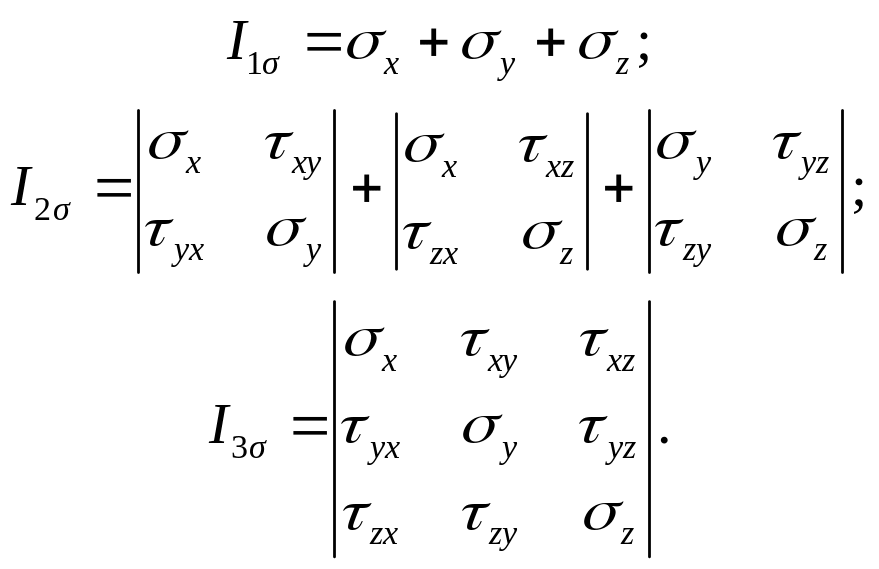(3.12)

Главные напряжения равны трем действительным корням уравнения (3.11). Они являются объективной характеристикой напряженного состояния материала в точке и не зависят от выбора системы координат. Поэтому величины являются постоянными и называются инвариантами напряженного состояния материала в точке.

Принята следующая индексация главных напряжений (рис. 3.3):

(3.13)

(1, 2, 3 – главные направления).

3

2

Рис. 3.3

Подставляя найденные значения в (3.9) и решая совместно системы уравнений (3.9), (3.9’), найдем величины и т.д., т.е. определим направления 1, 2, 3 главных напряжений (положение главных площадок).

Если в качестве исходной принять главную систему координат 1, 2, 3 (см. рис. 3.3), то выражения (3.4) для составляющих полного напряжения на произвольной площадке упрощаются: Тогда

(3.14)

Таким образом, векторы полных напряжений на площадках, проходящих через заданную точку, определяются эллипсоидом, полуосями которого являются главные напряжения (рис. 3.4).

Рис. 3.4

Отсюда следует, что являются экстремальными значениями полных напряжений на площадках, проходящих через заданную точку. Так как на главных площадках полные напряжения равны нормальным напряжениям, то . Если , то эллипсоид становится сферой и любая площадка вокруг рассматриваемой точки является главной.

В дальнейшем при изложении курса нам понадобятся соотношения для напряжений на характерных площадках.

Площадки, равнонаклоненные к главным, называются октаэдрическими. Их число равно восьми, и они образуют в окрестности исследуемой точки октаэдр. Для таких площадок , а напряжения на них одинаковы.

Пусть – нормаль на октаэдрической площадке. Из (3.4)–(3.7) следует:

(3.15)

где – среднее нормальное напряжение.

3.4. Виды напряженных состояний

В том случае, когда все три корня уравнения (3.11) не равны нулю, напряженное состояние называется трехосным или объемным.

В то же время нетрудно заметить, что существуют напряженные состояния, при которых один или два корня кубического уравнения (3.11) могут быть нулевыми. В частности, если , то уравнение (3.11) преобразуется к виду , один из корней равен нулю, а два другие – ненулевые. Такое напряженное состояние называется двухосным или плоским.

В случае, если , два из трех корней уравнения (3.11) равны нулю. Такое напряженное состояние называется одноосным или линейным.

Возможно также состояние, при котором . В таком случае уравнение (3.11) преобразуется к виду . Один из корней этого уравнения равен нулю, а два другие . Такое напряженное состояние является плоским и соответствует чистому сдвигу в какой-либо плоскости, например, в плоскости xy (рис. 3.5, а).

При сочетании чистых сдвигов в ортогональных плоскостях xy, xz, yz (рис. 3.5, б) напряженное состояние является объемным, причем .

Классифицируя напряженные состояния по формальному признаку, придем к следующим комбинациям:

Линейное напряженное состояние (ЛНС)

Плоское напряженное состояние (ПНС)

Объемное напряженное состояние (ОНС)

Реальные напряженные состояния являются объемными. Плоские и линейные напряженные состояния являются следствием использования упрощающих гипотез при определении напряжений на площадках, т.е. являются, по сути, расчетными схемами реальных напряженных состояний.