3. Теория напряженно-деформированного состояния материала в точке

3.1. Понятие о напряженном состоянии материала в точке. Тензор напряжений

Пусть тело, выполненное из твердого материала (рис. 3.1, а), деформируется при нагружении и в материале возникают дополнительные силы внутреннего взаимодействия.

Напряженным состоянием в точке K(x, y, z), принадлежащей деформируемому телу, называют совокупность напряжений на всевозможных площадках, проходящих через эту точку.

Выделим вокруг точки K(x, y, z) бесконечно малый элемент объема плоскостями, параллельными осям x, y, z заданной системы координат. В силу бесконечной малости объема напряженное состояние в нем можно считать однородным (т.е. одинаковым во всех точках объема), поэтому напряжения на его гранях характеризуют напряженное состояние в точке K(x, y, z).

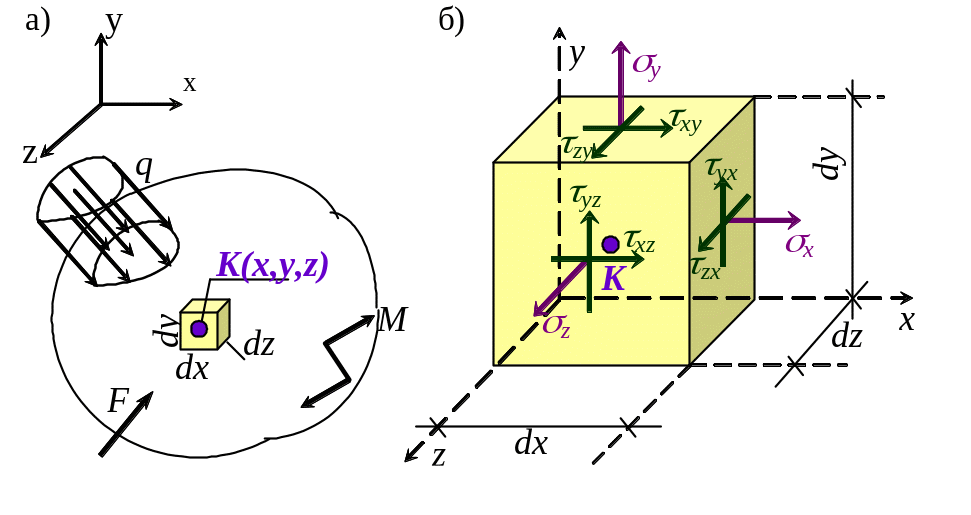
Рис. 3.1

Векторы напряжений на гранях выделенного элементарного параллелепипеда можно разложить по координатным направлениям x, y, z (рис. 3.1, б). Проекции на нормали к площадкам называются нормальными напряжениями. Проекции на направления в плоскостях площадок называются касательными напряжениями.

Правила знаков:

Нормальное напряжение считается положительным, если направлено в сторону внешней нормали к рассматриваемой площадке (соответствует растяжению). В противном случае оно отрицательно.

Касательное напряжение положительно, если при положительной (или отрицательной) ориентации внешней нормали к сечению вектор касательного напряжения также положительно (или отрицательно) ориентирован.

Тензором напряжений в точке K(x, y, z) называют совокупность нормальных и касательных напряжений на гранях выделенного элементарного объема. Эту совокупность удобно представить в виде квадратной матрицы:

. (3.1)

По главной диагонали располагаются нормальные напряжения, а каждый столбец характеризует напряжения на соответствующей грани выделенного элемента. Направления векторов нормальных и касательных напряжений на рис. 3.1, б, соответствуют их положительным значениям.

Тензор напряжений характеризует напряженное состояние материала в рассматриваемой точке и содержит девять составляющих полных напряжений на гранях выделенного элемента. Однако, рассматривая условия равновесия выделенного объема, можно составить только шесть уравнений. Таким образом, задача выявления напряженного состояния материала в точке три раза статически неопределима.

Составляя уравнения моментов относительно осей x, y, z, из условий равновесия выделенного элемента получим следующие соотношения:

(3.2)

Эти зависимости носят название закона парности касательных напряжений.

3.2. Напряжения на наклонной площадке

Для определения напряжений на произвольной площадке выделим из тела вокруг исследуемой точки элементарный тетраэдр, три грани которого параллельны координатным осям (рис. 3.2). Положение наклонной площадки abc зададим направляющими косинусами

Н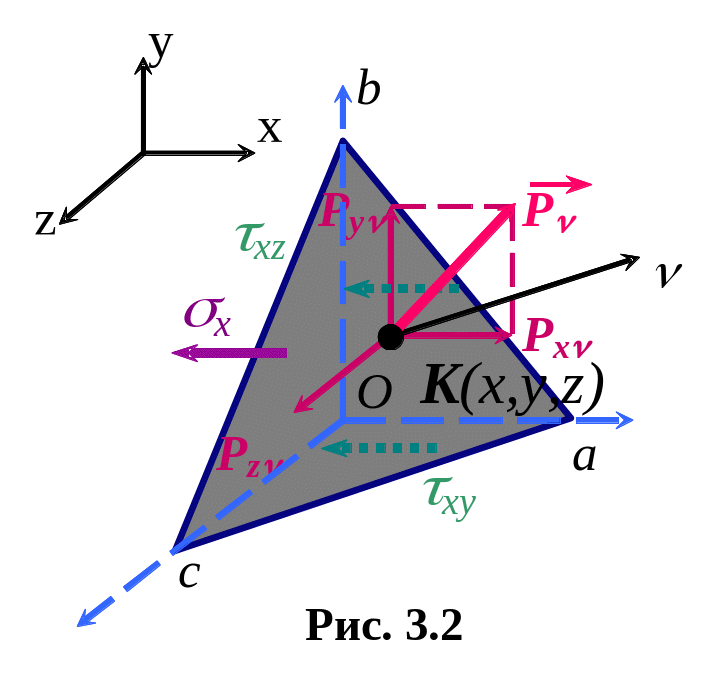 а рис. 3.2 вектор полного напряжения на наклонной площадке разложен по координатным направлениям, а на координатных плоскостях показаны только составляющие полных напряжений, параллельные оси X.

Проецируя на ось X все силы, действующие на вырезанный элемент объема, получим следующее уравнение равновесия:

(3.3)

где – площади соответствующих площадок. Так как , то, преобразуя (3.3), получим выражение для . Аналогично можно получить выражения для составляющих . Таким образом, выражения для составляющих полного напряжения на наклонной площадке имеют вид: