2.3. Понятие об эпюрах внутренних усилий в стержнях

Эпюрами внутренних усилий называют графики, показывающие величины (а часто и знаки) соответствующих усилий в сечениях стержней. Эпюры строятся на продольных осях стержней как на нулевых линиях. На эпюрах продольных сил (эп. N), поперечных сил (эп. , ) и крутящих моментов (эп. ) знаки ставятся. На эпюрах изгибающих моментов (эп. и ) знаки, как правило, не ставятся, и ординаты (абсолютные величины изгибающих моментов в сечениях) откладываются со стороны растянутых волокон.

При построении эпюр внутренних усилий рационально придерживаться следующего порядка работы.

1. Выбирается глобальная система координат X,Y,Z, в которой задаётся геометрия стержня, нагрузки и определяются опорные реакции.

2. Проводится разбиение стержня на грузовые участки. Под грузовым участком будем понимать часть стержня, на которой выражения для внутренних усилий в сечениях не меняются. На участках (при целесообразности) выбираются дополнительные локальные системы координат X_i,Y_i,Z_i (i – номер грузового участка), облегчающие составление выражений для внутренних усилий.

3. С использованием метода сечений составляются аналитические выражения для внутренних усилий в сечениях на грузовых участках. При этом необходимо приводить расчётную схему выделенной части стержня, на которой показывать выбранную на участке систему координат и заведомо положительные внутренние усилия в текущем сечении.

4. По найденным выражениям строятся графики – эпюры внутренних усилий в сечениях стержня.

Рис. 1.6

2.4. Примеры построения эпюр внутренних усилий в стержнях

Пример 2.1. Для стержня, расчетная схема которого представлена на рис. 2.9, а, требуется построить эпюру N.

Решение

1. Выделим грузовые участки стержня 1, 2.

2. В пределах каждого грузового участка рассматриваем сечения на расстоянии х_i от начала участка, т.е. используем локальные системы координат.

Рис. 2.9

3. Записываем функции продольных сил N_i(х_i) на участках. При этом рассматриваем свободную от опоры часть бруса.

1-й грузовой участок, 0 ≤ x ≤ 2 м.

,

кН (продольная сила на участке постоянна).

2-й грузовой участок, 0 ≤ x ≤ 3 м.

,

При м кН;

при м кН.

По вычисленным значениям строим эпюру N (рис. 2.9, б).

Пример 2.2. Для стержня, расчетная схема которого представлена на рис. 2.10, требуется построить эпюру

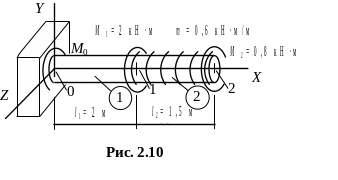
Решение

1. Отсекая стержень от опоры и составляя уравнение моментов относительно продольной оси X, получим:

.

Отсюда находим опорную реакцию:

кН·м.

2. Рассмотрим грузовые участки 1, 2.

1-й грузовой участок, 0 ≤ x ≤ 2 м.

;

кН∙м.

2 -й грузовой участок, 2 м ≤ x ≤ 3,5 м.

Отсюда

.

кН∙м;

кН∙м.

2. Используя полученные значения, строим эпюру (рис. 2.11).

.

Рис. 2.11

Пример 2.3. Для стержня, расчетная схема которого представлена на рис. 2.12, а), требуется построить эпюры = М и = Q.

Рис. 2.12

Решение

1. Выделяем грузовые участки 1, 2, 3, в пределах которых функции М_i(х), Q_i(х) не меняются.

2. В пределах грузовых участков рассматриваем произвольные сечения и вырезаем правую (относительно сечения) часть стержня.

3. Заменяя действие отброшенной части неизвестными положительными поперечной силой Q_i(x_i) и изгибающим моментом М_i(x_i) и рассматривая равновесие выделенной части балки, находим выражения внутренних усилий на участках

1-й грузовой участок,

Составим уравнения равновесия для 1-го участка:

= 0; Q₁(x₁) – qx₁+F = 0;

Приравнивая Q₁(х₁) к нулю при , получим:

Запишем уравнение для изгибающих моментов:

–М₁(х₁) – q +F x₁= 0;

м, Q₁(0)= –20;

м, кН∙м.

x₁ = 2,0 м, Q₁(2) = 10, кН∙м.

Аналогично находим выражения для внутренних усилий в сечениях на 2-м и 3-м грузовых участках:

2-й грузовой участок, м.

= 0; Q₂(x) – q 2 + F = 0; кН = const.

– М₂ (х₂) – q 2 (х₂+ ) + F (x₂+2) = 0;

кН∙м;

x₂ = 1,5 м, кН∙м.

3-й грузовой участок, м.

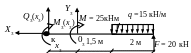
= 0; Q₃(x₃) – q · 2 + F = 0;

Q₃(x₃) = 10 кН= const.

Эпюра Q постоянна по длине участка.

–М₃(х₃) – М – qּ2(х₃+1+1,5)+F (x₃+3,5)=0;

кН∙м (знак «минус» означает, что растягиваются верхние волокна); x₃ = 1,0 м, кН∙м.

Эпюры М и Q, построенные по результатам расчётов, показаны на рис. 2.12 б, в.

Пример 2.4. Для ломаного пространственного стержня, изображенного на рис. 2.13, а, построить эпюры внутренних усилий.

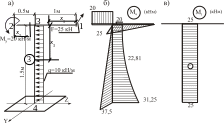
Рис. 2.13

Решение

При рассмотрении отсеченных частей стержня (см. рис. 2.13) условимся в данном случае не изображать графически неизвестные внутренние усилия в сечениях, попавших в разрез. Для обозначений внутренних усилий используем в качестве индексов локальные оси сечения , , а при составлении выражений для внутренних усилий введем локальные системы координат Х_i, Y_i, Z_i на грузовых участках.

1-й грузовой участок, 0 1 м.

На 1-м грузовом участке крутящие моменты и продольные силы в сечениях отсутствуют. Выражения для изгибающих моментов на этом участке имеют вид:

;

;

м; кНм

(растягиваются волокна со стороны отрицательной полуоси – Z_1, поэтому ординаты на эпюре М_И откладываем с той же стороны; см. рис. 2.13, б).

М (х₁) = 0; М = = 0; Q = –25 кН; N⁽¹⁾ = Q = 0.

2-й грузовой участок, 0 0,5 м.

На 2-м грузовом участке (см. рис. 2.13, а) поперечные силы, крутящие моменты и продольные силы в сечениях отсутствуют, так как на левую отсеченную части действует только внешний момент М_у = 20 кНм (рис. 2.14, б).

кН∙м; (растягиваются волокна со стороны положительной полуоси ).

3-й грузовой участок, 0 1,5 м.

На 3-м вертикальном грузовом участке тоже рассматриваем верхнюю отсеченную часть (рис. 2.14, в).

Изгибающие моменты – ;

, ;

м, кНм

(растягиваются волокна со стороны положительной полуоси );

;

, кНм;

м, кНм;

м, кНм (растягиваются волокна со стороны положительной полуоси (рис. 2.14, в).

Крутящий момент – М = М = –F₁1 м = –25 кНм.

Х₁,

F = 25 кН

Z₂

Y₂

х₂

X₂,

М_у = 20 кН м

2

0,5 м

1 м

1

2

3

q = 10 кН/м

Х₃,

Y₃

х₃

Z₃

F = 25 кН

в)

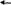
Рис. 2.14

Эпюра крутящих моментов М_t представлена на рис. 2.13, в.

N⁽³⁾ = 0; Q = –q x₃= –10x₃;

x₃ = 0, Q (0) = 0; x₃ = 1,5 м, Q (1,5) = 15 кН;

Q = F = 25 кН.

Эпюра поперечных сил представлена на рис. 2.13, г.