1.4. Деформации. Внутренние силы

Всякое изменение первоначальных размеров и формы тела при нагружении называется деформацией.

Различают деформации упругие и остаточные.

Упругие деформации исчезают после снятия нагрузки. Они связаны с обратимыми изменениями структуры материала.

Остаточные деформации связаны с необратимыми изменениями структуры материала и остаются после снятия нагрузки.

Более детальная характеристика деформаций тела и его частей с геометрических позиций будет дана в дальнейшем.

При деформировании изменяется первоначальная структура материала, из которого выполнено тело. Наряду с начальными силами взаимодействия между частицами материала, характеризующими его стабильную структуру, появляются дополнительные силы внутреннего взаимодействия между частицами материала, вызванные деформированием тела под нагрузкой. Эти силы стремятся восстановить первоначальную структуру материала, т.е. как бы отражают сопротивление материала деформированию. Именно от величины и распределения дополнительных сил внутреннего взаимодействия между частицами материала зависит надежность работы элементов конструкций при нагружении.

1.5. Понятие о стержне (брусе). Основные виды деформации стержня

Стержнем называется тело (рис. 1.6), один размер которого значительно больше двух других ( ).

Рис. 1.6. Пространственный стержень

Стержень может быть образован путем перемещения плоской фигуры A вдоль линии таким образом, чтобы центр тяжести фигуры (точка O) находился на линии , а плоскость фигуры А была перпендикулярна линии .

В том случае, если A = const, а линия – прямая, стержень называется прямым призматическим.

Различают следующие простые виды деформации (сопротивления) стержня: растяжение; сжатие; сдвиг; кручение; изгиб. Простые деформации являются расчетными схемами действительной деформации стержня, включающей все виды простых деформаций. При этом влиянием отброшенных видов деформации пренебрегают в силу их малости.

1.6. Гипотезы о характере деформирования и свойствах материалов. Основные упрощающие принципы

1. Деформации, как правило, считаются малыми, что позволяет пренебречь изменением геометрии нагружаемого тела при составлении уравнений равновесия и вести расчет по так называемой «недеформируемой» схеме.

2. Материалы элементов считаются сплошными, однородными, изотропными и линейно упругими (т.е. деформируются с сохранением линейной связи между параметрами нагружения и деформирования).

3. При рассмотрении деформирования тела под нагрузкой зачастую применимы следующие принципы.

Принцип суперпозиции (линейного наложения)

Характеристики состояния сооружения при действии нескольких нагрузок можно находить как линейную сумму соответствующих характеристик состояния сооружения при действии каждой из нагрузок в отдельности. Например, перемещение при действии сил на балку (рис. 1.7, а) можно находить как сумму величин , , т.е. (рис. 1.7, б, в).

Рис. 1.7. Пример использования принципа суперпозиции

Принцип Сен-Венана

Состояние материалов элементов конструкции при достаточном удалении от места приложения нагрузки не зависит от характера ее приложения. Иллюстрацией здесь могут служить случаи загружения балки нагрузкой через круглый и прямоугольный штампы (рис. 1.8). Эти загружения будут эквивалентными при малых величинах и могут быть представлены одинаковой расчетной схемой (рис. 1.8, в).

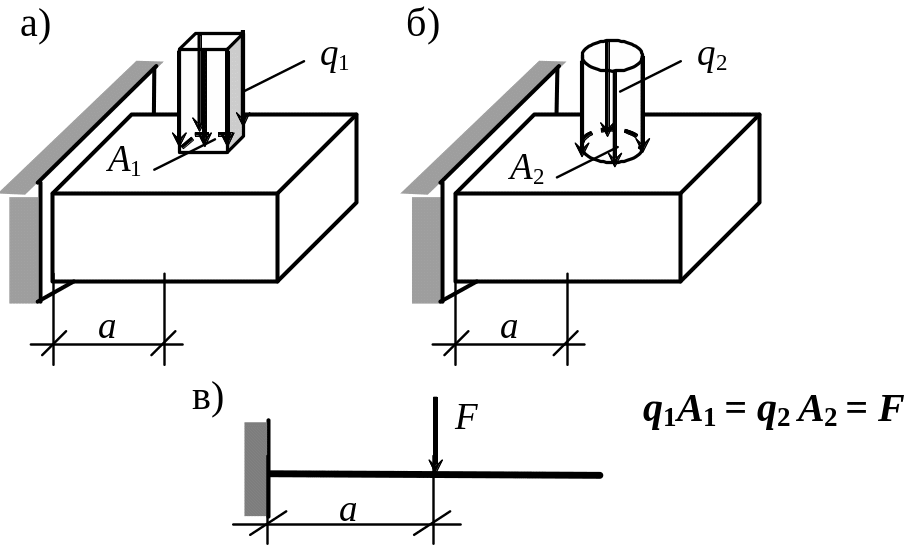
Рис. 1.8. Иллюстрация принципа Сен-Венана