7.5. Статически неопределимые задачи при кручении

В том случае, когда концы стержня, подвергающегося кручению, неподвижно закреплены (рис. 7.12), система является один раз статически неопределимой.

Рис. 7.12

Пусть n – число участков стержня (под участком i будем в данном случае понимать такую протяженность стержня, на которой функция не меняется; для круглых стержней ). Для определения опорных реакций M₀, M_n (крутящих моментов в сечениях 0, n) можно использовать только одно уравнение статики

(а)

при рассмотрении равновесия стержня (остальные тождественно выполняются).

Дополнительное уравнение находится из условия неподвижного закрепления сечения n: . Используя общее выражение для углов закручивания сечений на участках и учитывая, что получим

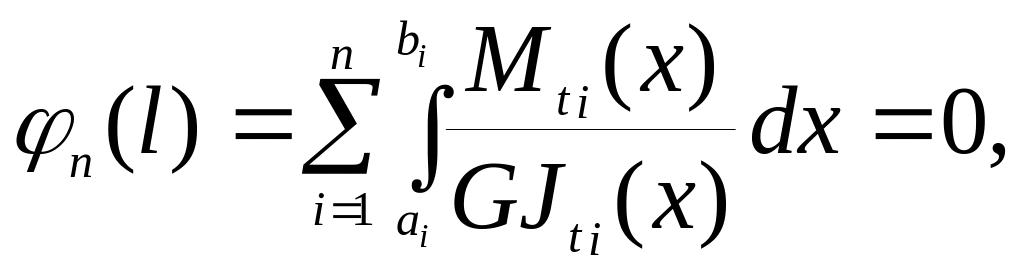(б)

где a_i, b_i – координаты начала и конца участка i.

Решая систему (а), (б), найдем M₀, M_n и, таким образом, статическая неопределимость разрешена. Удобно в данном случае определять выражения , вырезая, например, левую часть стержня. Тогда во все выражения , i = 1, 2, …, n, войдет только неизвестная величина M₀, и она определяется из решения уравнения (б), т.е. система (а), (б) разделится. Описанный выше алгоритм расчета используется при любом числе неподвижных закрепленных сечений. При этом необходимо решать m – 1 самостоятельных статически неопределимых задач для частей стержня между неподвижными закреплениями.

7.5.1. Учет линейно упругой податливости опорных связей

При закреплении стержня податливыми связями степень статической неопределимости системы может быть какой угодно.

Рис. 7.13

В случае наложения линейно упругих связей (рис. 7.13) неизвестная реакция в связи и угол закручивания сечения, на которое наложена эта связь, входят в соотношение

(7.40)

где – координаты сечения;

– жесткость связи.

Используя условия (7.40), получим дополнительные (к уравнениям статики) уравнения. Решая полученную систему уравнений, найдем реакции в наложенных связях, таким образом, статическая неопределимость разрешена. При этом, если на начальное сечение наложена упруго податливая связь (см. рис. 7.13), то

7.5.2. Примеры расчетов статически неопределимой системы различными методами

Рассмотрим статически неопределимую систему при кручении, образованную из ранее рассмотренной статически определимой системы (см. рис. 7.6, 7.14).

МПа, МПа, G = const.

Для упрощения выкладок будем полагать, что заданная расчетная нагрузка равна нормативной (коэффициенты перегрузки равны единице), а коэффициент запаса надежности (прочности) системы при расчете по несущей способности определяется только расчетным сопротивлением . При расчете по методу разрушающих (предельных) нагрузок также примем коэффициент запаса прочности по нагрузке равным 1,5.

Расчет по несущей способности (по прочности)

Для выявления крутящих моментов в поперечных сечениях проведем расчет рассматриваемой один раз статически неопределимой системы.

Рис. 7.14

1. Статическая сторона задачи

Отсечем стержень от опор и составим уравнение моментов всех силовых факторов, действующих на отсеченный стержень относительно оси x:

. (1)

Выражения для крутящих моментов на участках 1, 2, 3 имеют вид:

(а)

2. Геометрическая сторона задачи

Так как крайние сечения стержня неподвижно защемлены, то углы закручивания

и . (2)

Уравнение (2) обобщает геометрическую сторону данной задачи.

3. Физическая сторона задачи

Будем полагать, что материал стержня работает в пределах линейно упругих деформаций. Пользуясь зависимостью (7.18) и соотношениями (а), получим:

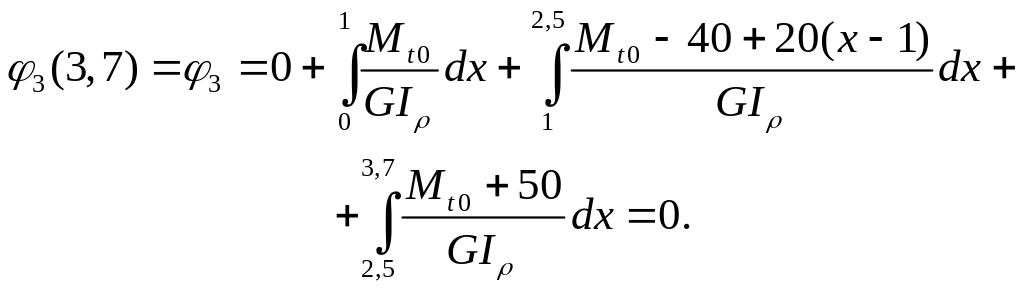(3)

Уравнение (3) обобщает геометрическую и физическую стороны задачи. После интегрирования и сокращения получим:

кНм.

Из (1) найдем кНм. Используя найденные значения , , построим эпюру крутящих моментов в сечениях (рис. 7.14, б).

Условие расчета по несущей способности (по прочности) для опасного сечения 1–1 можно записать следующим образом:

.

Для сечения, подобранного при расчете статически определимого стержня (рис. 7.6),

м³,

кНм > ; условие прочности выполняется с запасом. Подбирая сечение из условия , получим: ; м, т.е. требуемый диаметр сечения стержня в статически неопределимой системе, образованной из статически определимой, можно уменьшить.