7.4. Свободное кручение стержней, сечение которых составлено из прямоугольников

Сечения стержневых элементов строительных конструкций зачастую комбинируются из прямоугольников. К подобным элементам относятся, прежде всего, сварные стержни, выполненные из полос листовой стали. Сечения прокатных элементов также можно приближенно представить в виде набора прямоугольников.

Профильные линии

а) б) в) г) д)

Рис. 7.10

Один из размеров прямоугольников, составляющих поперечное сечение, как правило, значительно больше другого. Центральные оси прямоугольников, параллельные длинным сторонам, образуют профильную линию сечения. В том случае, если профильная линия не замкнута, профиль называется открытым (рис. 7.10, а, б), в противном случае – замкнутым (или закрытым, рис. 7.10, в, г). Рассматриваемая теория расчета стержней замкнутого профиля не требует, чтобы поперечное сечение было составлено только из прямоугольников (рис. 7.10, д).

7.4.1. Кручение стержней открытого профиля

Расчет на свободное кручение стержней открытого профиля, сечение которых составлено из прямоугольников, можно провести на основе вышеизложенного решения Сен-Венана и принципа суперпозиции.

Пусть n – число прямоугольников. Тогда общий крутящий момент в сечении представляется в виде суммы

(7.29)

где , i = 1, 2, …, n – части, приходящиеся на отдельные прямоугольные полоски. Считая, что контур сечения при закручивании не деформируется, получим

(7.30)

Из (7.30) следует

(7.31)

В случае, если полоски выполнены из одного материала:

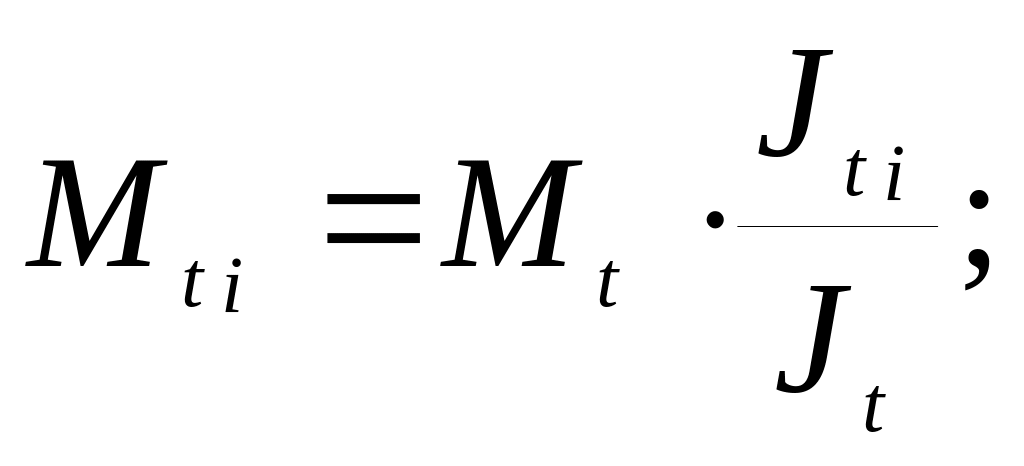
(7.32)

Для прокатных стержней вводятся поправочные коэффициенты, т.е. , где величина зависит от формы сечения (для двутавра = 1,2, для швеллера = 1,12). Максимальное касательное напряжение в сечении i-й полоски равно

(7.33)

Составляя условие прочности, получим

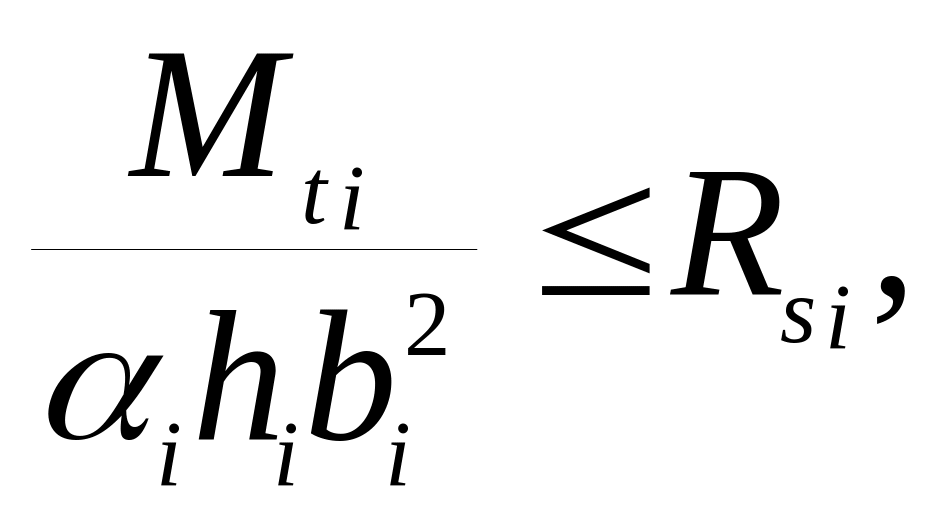i = 1, 2, …, n. (7.34)

При соотношении , . Для стержня, выполненного из одного материала,

(7.35)

т.е. максимальное касательное напряжение будет в самом толстом прямоугольнике. Условие прочности имеет вид

(7.36)

Соотношение (7.36) служит и для подбора сечений (при заданном соотношении толщины полос и заданных соотношениях ).

Учитывая, что жесткость сечения при кручении в данном случае определяется суммой (7.31), при определении углов закручивания и проверке жесткости можно использовать ранее описанную методику.

7.4.2. Кручение стержней замкнутого профиля

В зависимости от очертания профильной линии различают односвязные и многосвязные профили. В случае односвязного профиля профильная линия замыкает только одну подобласть плоскости поперечного сечения (рис. 7.11).

Дифференциальное уравнение кручения стержня односвязного профиля имеет вид

(7.37)

где – момент инерции текущего сечения;

– удвоенная площадь подобласти, ограниченной профильной линией;

– толщина профиля в точке с координатой S вдоль профильной линии;

О – начало отсчета координаты S.

Рис. 7.11

При малой толщине профиля (L – длина продольной линии) можно полагать, что касательные напряжения направлены вдоль профильной линии и равномерно распределяются по толщине профиля (рис. 7.11). Тогда

(7.39)

Определение углов закручивания сечений и проверка жесткости стержня проводится так же, как и при рассмотрении круглых стержней, с заменой величины на величины на участках. На основе составленных условий прочности и жесткости решаются поверочные задачи и проектные задачи подбора сечений и нагрузок.