1. Основные понятия, гипотезы и принципы, используемые в сопротивлении материалов

1.1. Расчетная схема сооружения

Под «сооружением» будем в дальнейшем понимать любой объект, выполненный из твердых деформируемых материалов, имеющий определенное функциональное назначение и воспринимающий заданную нагрузку (жилой дом, промышленное здание, мост, автомобиль и т.д.). Сооружение может быть разделено на части – конструкции, а те, в свою очередь – на элементы.

Расчетной схемой называют идеализированное (упрощенное) представление реального сооружения или отдельной его части. Идеализация (упрощения) должна проводиться таким образом, чтобы сохранялись основные свойства реального сооружения, а все упрощения шли бы в запас его надежности. В качестве примера представления части сооружения его расчетной схемой можно привести, например, ригель сборного каркаса здания (рис. 1.1).

а)

б)

Рис. 1.1. Ригель каркаса здания (а) и его расчетная схема (б)

Понятие «расчетная схема» относится не только к представлению геометрии сооружения и его связей со средой, но и к его нагружению и физическим свойствам материалов элементов.

Как видно из рис. 1.1, ригель на расчетной схеме представлен прямой продольной осью, а его соединения с колоннами считаются шарнирными, т.е. допускают свободный поворот опорных сечений. Это не согласуется с реальными условиями соединения ригеля с колоннами, но упрощает расчет и идет в запас надежности.

1.2. Типы связей (опор)

Различают недеформируемые и деформируемые связи между отдельными телами, элементами и частями сооружения, сооружением и средой. Недеформируемые связи, как правило, являются расчетной схемой реальных деформируемых связей. Простейшая недеформируемая связь представлена на рис. 1.2.

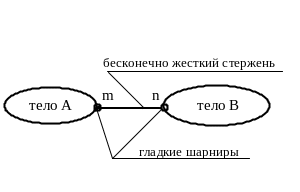
Рис. 1.2. Простейшая недеформируемая связь

Подобная связь называется линейной. Она отнимает взаимную линейную подвижность тел А и В в направлении m-n.

Любую недеформируемую связь между телами можно скомбинировать в расчетной схеме из линейных связей. В том случае, если эти линейные связи располагаются в одной плоскости, представляемая связь называется плоской, в противном случае – пространственной. Связи изучаемых деформируемых тел с «землей» (массивным телом, которое, как правило, в расчетной схеме считается абсолютно жестким) называются опорами. Примеры плоских недеформируемых опор показаны на рис. 1.3.

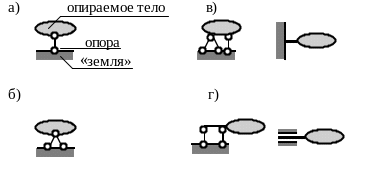
Рис. 1.3. Типы плоских опор:

а) шарнирно подвижная опора; б) шарнирно неподвижная опора; в) неподвижное защемление; г) подвижное защемление

Д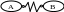 еформируемые связи имеют специальные обозначения. Например, упругая деформируемая связь между телами А и В изображается в виде пружины:

Из деформируемых связей могут быть скомбинированы деформируемые опоры.

1.3. Классификация нагрузок

По физической природе все нагрузки делятся на следующие виды: силовые; температурные; «неточность» изготовления и монтажа; смещение опорных связей.

По характеру приложения во времени различают нагрузки статические и динамические.

Нагрузка считается статической, если передается на сооружение без появления скоростей и ускорения масс. Статические нагрузки являются расчетными схемами реальных нагрузок в том случае, когда скорости и ускорения масс незначительны. В противном случае нагрузки считаются динамическими.

По характеру приложения в пространстве силовые нагрузки подразделяются на сосредоточенные и распределенные.

а)

б)

Рис. 1.4. Сосредоточенные силовые нагрузки

Сосредоточенная нагрузка передается на сооружение в точке. Различают два вида сосредоточенных силовых нагрузок: сосредоточенная сила F; сосредоточенная пара сил с моментом М (рис. 1.4).

Рис. 1.5. Распределенные силовые нагрузки

Сосредоточенные силовые нагрузки являются расчетными схемами реальных нагрузок, передающихся на сооружение по малой поверхности. Они характеризуются величиной, точкой приложения и направлением.

Распределенные нагрузки передаются на сооружение по линии, поверхности или объему (рис. 1.5).

Они характеризуются областью приложения (линия m-n, поверхность S, объем V), величиной интенсивности q и направлением. Интенсивность и направление распределенной нагрузки могут быть как постоянными, так и переменными (функциями координат точек приложения).