7.2.2. Определение углов закручивания сечений. Расчет по деформациям (на жесткость)

Используя соотношение, найденное при рассмотрении всех трех сторон задачи определения напряжений, получим дифференциальное уравнение для углов закручивания сечений:

(7.17)

где – искомая функция углов закручивания сечений;

– функции крутящих моментов и жесткостей сечений при кручении.

Пусть n – число участков интегрирования, i = 1, … , n, – функции крутящих моментов и жесткостей сечений при кручении на участках. Из соотношения (7.17) следует, что угол взаимного закручивания крайних сечений i-го участка равен 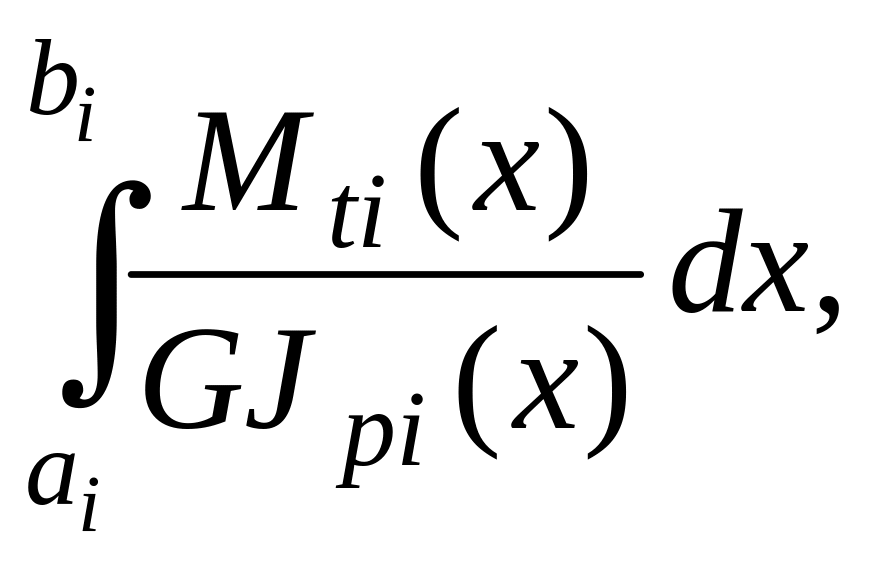где a_i, b_i – координаты начала и конца участка «i» в выбранной, единой для всех участков, системе координат. Используя для интегрирования уравнения типа (7.17) методику определенного интеграла, получим зависимость для углов закручивания на произвольном участке j:

j = 1,.., n, (7.18)

где – угол закручивания начального сечения.

Зависимость (7.18) позволяет построить эпюру углов закручивания сечений стержня (рис. 7.6, в).

Расчет по деформациям (на жесткость), согласно нормам проектирования, как было отмечено в разделе 4, проводится по нормативным нагрузкам. Условие жесткости по углу закручивания имеет вид:

(7.19)

где – максимальный по модулю угол закручивания для сечений стержня от нормативной нагрузки;

– допустимая величина угла закручивания.

Используя зависимость (7.18), построим эпюру углов закручивания сечений круглого стержня, представленного на рис. 7.6, и проверим его жесткость. Коэффициенты перегрузки будем считать равными единице; G = 0,8 · 10⁵ МПа = 0,8 · 10⁸ кН/м² (сталь); рад.

Согласно (7.19), условие жесткости рассматриваемого стержня записывается в виде . Принимая сечение круглого стержня, подобранное ранее по условию прочности, получим:

рад < .

Таким образом, при заданном значении рад условие жесткости стержня выполняется.

Если, например, рад, то условие жесткости круглого стержня, сечение которого подобрано ранее по прочности, не выполняется. В таком случае требуется корректировка сечения по условию жесткости. В рассматриваемом примере из условия жесткости следует:

м,

что больше значения r = 0,083 м, полученного ранее из условия прочности.

7.2.3. Расчет по разрушающей (предельной) нагрузке

Будем полагать, что зависимость при сдвиге описывается диаграммой Прандтля для идеально жестко-пластического материала (рис. 7.7).

Рис. 7.7 Рис. 7.8

Эпюры касательных напряжений в поперечных сечениях круглого и круглого трубчатого сечений в предельном состоянии показаны на рис. 7.8. Определяя сумму моментов сил внутреннего взаимодействия относительно точки О, найдем предельные крутящие моменты в поперечных сечениях:

– для круглого стержня

(7.20)

– для круглого трубчатого стержня

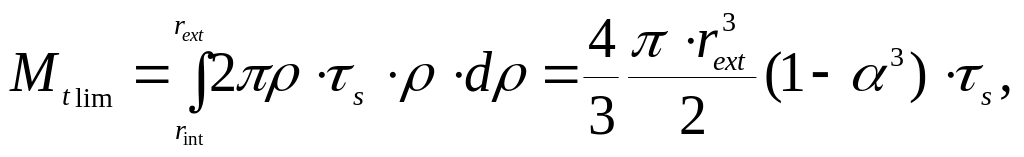(7.21)

где – предел текучести материала при сдвиге.

Величину предельного крутящего момента удобно представить в виде

, (7.22)

где – пластический момент сопротивления сечения. Нетрудно заметить, что для круглого сечения , а для кольцевого сечения . Пусть М – параметр нагружения. Условие расчета по предельной нагрузке имеет вид:

(7.23)

где – коэффициент запаса прочности по нагрузке;

– максимальный крутящий момент в сечении от заданной нормативной нагрузки. Условие (7.23) позволяет решить как поверочную, так и проектные задачи (подбор сечений, подбор нагрузок).