7. Кручение прямых стержней

Кручением называется деформация прямого стержня при действии нагрузок в виде пар сил, плоскости которых перпендикулярны продольной оси стержня. Деформация кручения является основной при расчете валов и пружин. При расчете элементов строительной конструкции деформация кручения, как правило, сочетается с другими видами деформации (осевое растяжение-сжатие, изгиб, сдвиг).

7.1. Определение усилий в поперечных сечениях

В случае кручения прямого стержня (рис. 7.1) силы внутреннего взаимодействия в поперечном сечении суммируются к одному внутреннему силовому фактору – крутящему моменту M_t.

Рис. 7.1

Правило знаков: крутящий момент M_t в сечении считается положительным, если при взгляде со стороны внешней нормали к сечению пара сил, ему соответствующая, как бы вращает выделенную часть стержня по часовой стрелке.

При построении эпюры M_t в статически определимой системе достаточно воспользоваться методом сечений и уравнением моментов . Например, для сечений с координатами a ≤ x ≤ a + b (см. рис. 7.1, участок 2)

, (7.1)

где m(x) – интенсивность распределенной моментной нагрузки.

С использованием найденных выражений M_ti(x), i = 1,…, n (n – число участков), строится эпюра M_t.

7.2. Кручение стержней круглого и кольцевого сечений

Опытное изучение кручения круглого и кольцевого сечений позволило выявить следующее:

1) поперечные сечения в процессе закручивания остаются плоскими и перпендикулярными продольной оси стержня; размеры и форма сечений не меняются;

2) радиусы поперечных сечений остаются прямыми;

3) расстояния между поперечными сечениями не меняются.

Сформулированные положения позволяют существенно упростить задачу определения напряженно-деформированного состояния круглых стержней.

7.2.1. Определение напряжений в поперечных сечениях. Расчет на прочность

Выделим из стержня круглого сечения элементарный участок dx с постоянным крутящим моментом M_t в сечениях (рис. 7.2).

Рис. 7.2

Согласно приведенным выше характеристикам деформации стержня, нормальные напряжения в показанных сечениях отсутствуют (в силу отсутствия линейных деформаций продольных волокон), а векторы касательных напряжений перпендикулярны радиусам. Для выявления зависимости τ(ρ) рассмотрим три стороны задачи.

1. Статическая сторона задачи

Рассмотрение этой стороны задачи сводится, в данном случае, к составлению условия суммирования касательных сил взаимодействия в поперечном сечении к закручивающей паре с моментом M_t (крутящий момент в сечении):

(7.2)

Сформулированная таким образом задача определения напряжений τ(ρ) в точках поперечного сечения является бесчисленное множество раз статически неопределимой.

2. Геометрическая сторона задачи

С учетом сформулированного выше рассмотрим деформацию выделенного участка стержня длиной dx, полагая левое сечение условно неподвижным (рис. 7.3).

Рис. 7.3

В силу малости угла сдвига

. (а)

Так как

(б)

то, подставляя (б) в (а), получим:

(7.3)

Соотношение (7.3) является уравнением неразрывности деформаций для данного случая деформации стержня и обобщает геометрическую сторону рассматриваемой задачи.

3. Физическая сторона задачи

Выделим из стержня элемент объема плоскостями поперечных сечений, плоскостями, содержащими радиусы , и плоскостями, перпендикулярными (рис. 7.4).

Рис. 7.4

Так как нормальные напряжения на площадках выделенного элемента отсутствуют, он находится в состоянии чистого сдвига, и по закону Гука

(7.4)

где G – модуль сдвига материала стержня. Учитывая (7.3), получим:

(7.5)

Зависимость (7.5) объединяет геометрическую и физическую стороны рассматриваемой задачи. Подставляя (7.5) в (7.2), проведем дальнейшие преобразования:

При G = const

Величина – полярный момент инерции сечения. Следовательно:

(7.6)

Подставляя (7.6) в (7.5), получим формулу, которая описывает закон распределения касательных напряжений в поперечном сечении круглого стержня при кручении:

(7.7)

На рис. 7.5 приведены эпюры, иллюстрирующие зависимость (7.7) в случаях круглых и круглых трубчатых стержней. Величина максимального касательного напряжения в сечении равна

(7.8)

где – полярный момент сопротивления;

– крутящий момент в сечении от расчетной нагрузки.

Рис. 7.5

Для круглого сечения

(7.9)

В случае кольцевого сечения

(7.10)

где

Как было показано ранее, напряженное состояние в точках деформируемого круглого стержня при кручении соответствует чистому сдвигу. В таком случае в опасной точке стержня Используя третью теорию прочности, получим следующее условие расчета по несущей способности (условие прочности):

(7.11)

где R_S – расчетное сопротивление при сдвиге;

R – основное расчетное сопротивление материала.

Для стержней постоянного сечения . Тогда условие прочности (7.11) записывается в виде:

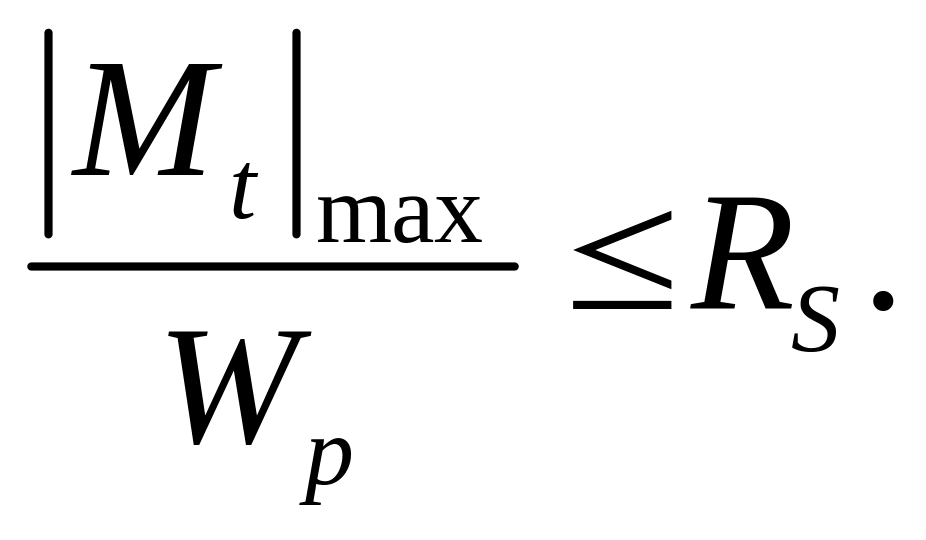(7.12)

Условие (7.12) позволяет решать как поверочную, так и проектные задачи расчета на прочность. Условие подбора сечения по прочности имеет вид:

(7.13)

Учитывая (7.9) и (7.10), получим условия для подбора размеров сечений:

– для круглого стержня

(7.14)

– для круглой трубы

(7.15)

При проектировании нагружения используется условие

. (7.16)

Пример расчета

Для стержня, изображенного на рис. 7.6, при заданной расчетной нагрузке, подобрать круглое и круглое трубчатое сечение по условию прочности при R_S = 100 МПа = 100 · 10³ кН/м².

а)

б)

Эп. M_t

в)

Эп. 

Рис. 7.6

Эпюра крутящих моментов в сечениях представлена на рис. 7.6 (б).

Согласно (7.14) и (7.15),

м; ;

м; .

Сравнивая площади полученных сечений, можно убедиться, что стержень трубчатого сечения в 3,98 раза экономичнее (по расходу материала) стержня круглого сечения и его предпочтительнее использовать для стержней, подверженных кручению.