6. Геометрические характеристики плоских сечений

Площадь поперечного сечения стержня А (м²) является наиболее простой интегральной геометрической характеристикой плоского сечения, применяемой в расчетах стержней на прочность и жесткость при растяжении и сжатии, при определении напряжений, потенциальной энергии деформации и др.: , где – элементарная площадка поперечного сечения стержня.

При расчетах стержней, испытывающих деформацию изгиба и кручения, в случае сложного сопротивления и при расчете сжатых стержней на устойчивость применяются усложненные интегральные геометрические характеристики плоских сечений. К подобным геометрическим характеристикам относятся: статический момент площади сечения; полярный, осевой (экваториальный) и центробежный моменты инерции сечения. Их величины зависят от формы и размеров сечения, от положения осей и полюсов, относительно которых они вычисляются.

Для сечений простой формы (прямоугольной, круглой сплошной, кольцевой и т.д.) геометрические характеристики определяются по сравнительно простым формулам. Для стержней прокатных профилей (уголковые, швеллерные, двутавровые и др.) они определяются согласно ГОСТу на соответствующий сортамент и размещаются в таблицах сортамента.

Геометрические характеристики сложных сечений определяются как алгебраические суммы соответствующих характеристик простых сечений, составляющих сложное.

6.1. Основные интегральные характеристики плоских сечений

Статическим моментом площади плоского сечения относительно некоторой оси называется интегральная сумма произведений элементарных площадок на расстояния от этих площадок до соответствующей оси, взятая по всей площади :

(6.1)

где и – статические моменты относительно осей z и y.

О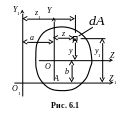 пределим статический момент сечения относительно осей z и y, параллельных осям z₁, y₁ (рис. 6.1).

По рисунку видно:

Тогда

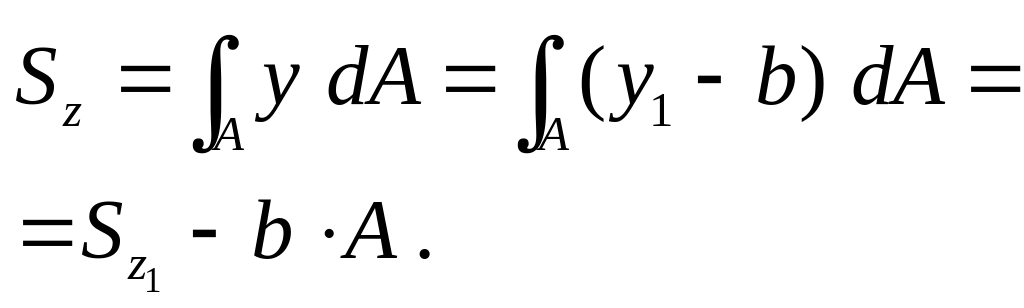По аналогии получим . Итак:

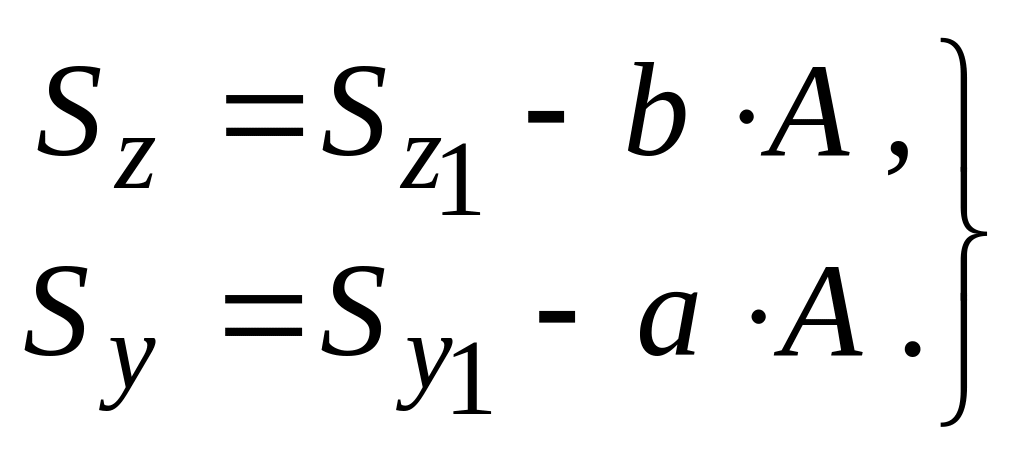. (6.2)

Найдем положение осей и , относительно которых статические моменты равны нулю. Для этого приравняем нулю выражения (6.2), приняв :

Отсюда

. (6.3)

Точка О пересечения осей z и y (рис. 6.2) называется центром тя­же­с­ти сечения. Оси, про­ходящие через центр тяжести сечения, назы­ваются центральными (или собственными) осями. Координаты центра тяжести определяются по формулам (6.3), из которых следует, что относительно любой центральной ( или собственной) оси статический момент сечения равен нулю.

Если известны площади частей сечения и координаты их центров тяжести, то координаты центра тяжести всего сечения в системе произвольных прямоугольных осей координат Z₁O₁Y₁ определяются по формулам:

(6.4)

где – координаты центров тяжести n частей сечения.

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется интегральная сумма произведений элементарных площадок на квадраты расстояний от этих площадок до полюса, взятая по всей площади А:

(м⁴). (6.5)

Значения положительны, поскольку и всегда больше нуля.

Осевым (экваториальным) моментом инерции сечения относительно некоторой оси (рис. 6.3) называется интегральная сумма произведений элементарных площадок на квадраты расстояний от этих площадок до соответствующей оси, взятая по всей площади А:

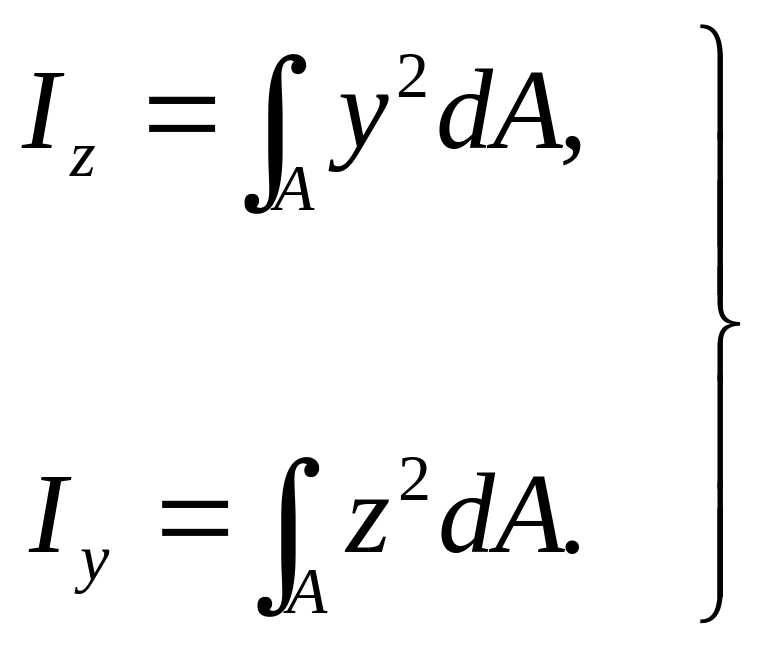(м⁴) (6.6)

З начения и также положительны.

Центробежным моментом инерции сечения относительно некоторых двух взаимно перпендикулярных осей (рис. 6.3) называется интеграль­ная сумма произведений элементарных площадок на расстояния от этих площадок до обеих осей, взятая по всей площади А:

, (м⁴) (6.7)

Значение может быть положительным, отрицательным или равным нулю, так как оно связано со знаками z и y.

Поскольку (см. рис. 6.3), то, подставляя в выражение (6.6) вместо сумму , получим:

. (6.8)

Таким образом, сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей.