5.6. Понятие о новых теориях прочности

Так как теорий прочности достаточно много, то подбор критерия достижения предельного состояния для данного материала является отдельной экспериментально-теоретической задачей. Поэтому вплоть до настоящего времени предпринимаются попытки построить объединенную теорию прочности.

5.6.1. Теория прочности Давиденкова – Фридмана

Эта теория прочности базируется на том, что в зависимости от вида напряженного состояния материал может разрушаться как хрупко – путем отрыва, так и вязко – путем среза. Соответствующие критерии разрушения имеют вид:

(5.20)

где – сопротивление отрыву; – сопротивление срезу.

Выражения (5.20), (5.21) совпадают с критериями разрушения по второй и третьей теориям прочности.

Предельные характеристики и характеристики напряженного состояния материала иллюстрируются на двух диаграммах (рис. 5.4).

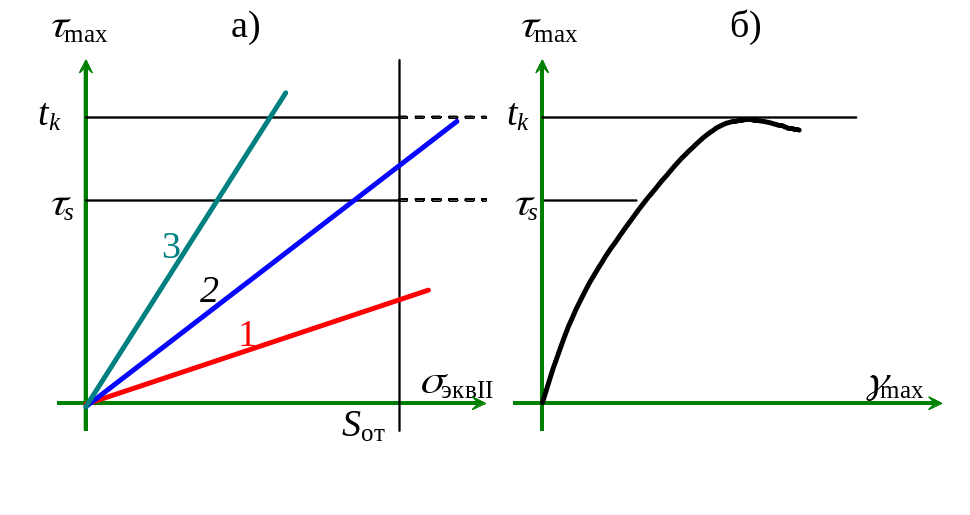
Рис. 5.4

В качестве предельной характеристики следует принимать величину временного сопротивления материала , найденную из опыта на растяжение. Величина превышает предел текучести при срезе и соответствует максимальным касательным напряжениям в предельном состоянии разрушения (рис. 5.4, б).

Для характеристики вида напряженного состояния принята величина (коэффициент мягкости)

.

На рис. 5.4, а прямые 1, 2, 3 соответствуют различным напряженным состояниям, причем . Прямая 1 соответствует напряженному состоянию, при котором материал разрушается путем отрыва, без предварительной пластической деформации. В состоянии 2 материал разрушается также путем отрыва, но с предварительной пластической деформацией. Прямой 3 соответствует разрушение путем среза. В первых двух случаях условия прочности вытекают из второй теории прочности (условие (5.5); в случае 3 условие прочности вытекает из третьей (или четвертой) теорий прочности (условия (5.9), (5.13)).

5.6.2. Объединенные теории прочности

При построении вышеприведенных теорий прочности выявлялись условия наступления предельного напряженного состояния, выраженные через главные напряжения . Условия прочности по различным теориям могут быть записаны в общем виде:

, (5.21)

где – вектор констант материала, определяемых экспериментально. Построение новых теорий осуществляется путем отыскания такой функции F в (5.21), которая позволяла бы полнее учесть механические свойства материала, работающего в условиях сложного напряженного состояния.

В настоящее время таких теорий (критериев) прочности достаточно много. Одной из наиболее общих является теория прочности Биргера, согласно которой

, (5.22)

где - интенсивность нормальных напряжений (5.14), – параметры, зависящие от свойств материала. Общность критерия Биргера заключается в том, что при определенных значениях из него следуют все известные линейные критерии прочности. Например, при , получаем критерий максимальных касательных напряжений; при , – энергетическую теорию прочности и т.д.

Для определения параметров , требуется проведение четырех базовых экспериментов: из опыта на растяжение определяют , на сжатие – , на кручение – . Четвертым проводят испытание тонкостенных труб под внутренним давлением. Этот опыт позволяет определить разрушающее окружное напряжение при внутреннем давлении . Тогда параметры материала:

(5.23)

Так как величина влияет только на , а влияние в случае сложного напряженного состояния наименее значительно, то для многих материалов можно принять .

Этот критерий, как и многие другие, пока не получил широкого применения в расчетной практике, но хорошо соответствует экспериментальным данным для ряда материалов. Разработка новых критериев предельного состояния, удобных для практического использования, является в настоящее время актуальной задачей.