4.5.3. Расчет по разрушающим предельным нагрузкам

Идея метода расчета конструкций по разрушающим (предельным) нагрузкам основана на предварительном выявлении параметра разрушающей (предельной) нагрузки . Условие надежной работы конструкции записывается в следующем виде:

, (4.24)

где – параметр заданной нормативной нагрузки;

K > 1– коэффициент запаса прочности по нагрузке, учитывающий все факторы, снижающие надежность работы конструкции.

П рименение метода разрушающих нагрузок имеет смысл, прежде всего, для пластичных материалов. При этом принимаются схематизированные диаграммы зависимостей при растяжении-сжатии (диаграммы Прандтля). Самый общий случай диаграммы Прандтля для материала с различными пределами текучести , при растяжении и сжатии представлен на рис. 4.19: а – диаграммы идеально упругопластического материала; б – диаграммы идеально жесткопластического материала. Для строительных сталей .

Рис. 4.19

Используются диаграммы Прандтля при определении предельной нагрузки соответствующей предположению, что при достижении нормальным напряжением предела текучести материал не разрушается, а неограниченно деформируется при постоянном напряжении, равном соответствующему пределу текучести. Соответственно, предельным будет такое состояние конструкции, при котором материал либо всюду течет, либо конструкция превращается в механизм. Выявление предельного состояния конструкции (разрушающей нагрузки) наиболее просто осуществляется для стержней и стержневых систем при растяжении-сжатии. Расчет по разрушающим нагрузкам позволяет экономить материал в случае расчета статически неопределимых систем (см. раздел 4.6).

4.6. Примеры решения поверочных и проектных задач при расчетах по предельным состояниям и разрушающим нагрузкам

Пример 1. Проиллюстрируем методики расчета по предельным состояниям на примере ранее рассмотренной системы (см. рис. 4.3).

Рис. 4.20

Пусть заданная нагрузка является нормативной, заданы коэффициенты перегрузки (рис. 4.20, а), расчетные сопротивления материала стойки при растяжении и сжатии МПа, МПа, а также модуль упругости материала МПа и площади сечений стойки м²; м² на участках.

Расчеты по несущей способности. Поверочная задача

Эпюры продольных сил и нормальных напряжений в сечениях стойки при действии расчетной нагрузки представлены на рис. 4.20, б, в. Составляя условия расчета по несущей способности, получим:

МПа > ; МПа > .

Таким образом, условия расчета по несущей способности не выполняются и в растянутой, и в сжатой зонах стержня, и требуется увеличить площади сечения , на участках.

Проектная задача 1. Подбор сечений

Будем подбирать площади сечений , на участках с сохранением соотношения : = 2. Тогда . Из условий расчета по несущей способности получим:

, м²;

,

Принимаем м²; м².

Проектная задача 2. Подбор нормативной нагрузки

Пусть нормативная нагрузка задана параметром . Тогда . Составляя условия расчета по несущей способности для опасных сечений в зонах растяжения и сжатия, получим:

кН;

кН.

Таким образом, если сечения стержня не менять, то нормативная нагрузка не должна превышать значений:

кН; кН/м.

Расчет по деформациям

Расчет по деформациям проводится, как правило, после расчета системы по несущей способности и с учетом его результатов. Будем полагать, что решена проектная задача 1 для системы, приведенной на рис. 4.20, и найдены новые площади сечений на участках м², м².

Пусть задано допустимое значение продольного перемещения сечения м. Согласно эпюре перемещений сечений от нормативной нагрузки при начальных площадях сечений м²; м² (рис. 4.3, г) Так как в данном случае перемещения сечений обратно пропорциональны параметру площади сечений, то необходимо определить величину с учетом результатов решения проектной задачи 1:

м > , т.е. условие расчета по деформациям (условие жесткости) не выполняется. Корректируя сечения по условию жесткости, получим: м².

Принимаем окончательно: м²; м².

Пример 2. Рассмотрим стержневую систему, расчетная схема которой приведена на рис. 4.21.

м;

; МПа;

м²; м²;

МПа.

По разрушающим нагрузкам коэффициент запаса прочности K = 1,5.

Р

Рис. 4.21

ассматриваемая система имеет условно неопределимую часть 1–2–3, шарнирно-неподвижно закрепленную в узле 1 и подкрепленную стержнями конечной жесткости 1, 2, работающими при растяжении-сжатии. Для упрощения выкладок будем полагать, что коэффициенты перегрузки . Поэтому надежность работы системы при расчете по несущей способности обеспечивается только расчетным сопротивлением материала (сталь) с коэффициентом запаса 1,5, равным требуемому коэффициенту запаса прочности при расчете по разрушающим предельным нагрузкам.

Поверочный расчет по несущей способности

Расчет по несущей способности необходимо начинать с определения усилий , в заданной один раз статически неопределимой системе.

Статическая сторона задачи

Используя сечение, показанное на рис. 4.23, и составляя сумму моментов относительно узла 1, получим:

. (1)

Геометрическая сторона задачи

Анализируя схему возможной деформации системы (рис. 4.22), получим:

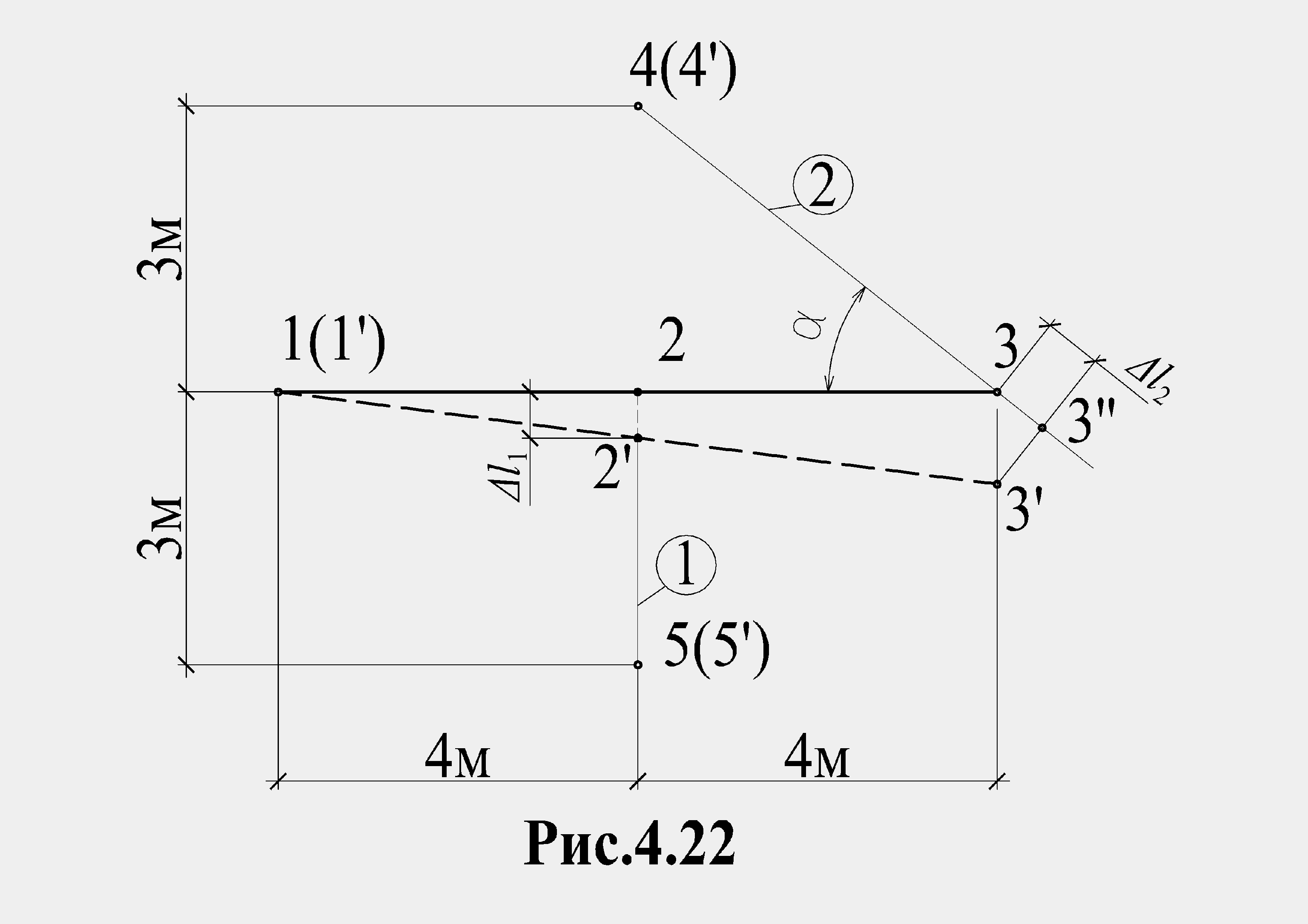, (а)

, (б)

(в)

Учитывая (а), (б), (в), найдем соотношение между , :

;

Рис. 4.22

(2)

Физическая сторона задачи

Считаем, что справедлив закон Гука. Тогда

(3)

Подставляя (3) в (2), получим:

. (4)

Решая систему (1), (4), получим:

кН; кН.

Условия прочности по несущей способности стержней 1, 2:

кН/м² = 42,2485 МПа << R;

МПа << R, т.е. стержни по условиям прочности значительно недогружены.

Проектный расчет по несущей способности при

Так как соотношение жесткостей стержней 1, 2 не меняется, то при расчете на силовую нагрузку усилия в них не меняются. Требуемые площади сечений можно определить из условий:

, м²;

, м².

Принимаем окончательно м²; м².

Проверочный расчет по разрушающей нагрузке при м²; м²

Выберем в качестве параметра внешней нагрузки . Тогда . Схема предельного состояния рассматриваемой системы представлена на рис. 4.23. Составляя уравнение моментов относительно т. 1, получим:

,

кН/м.

Рис. 4.23

Условие расчета по разрушающей (предельной) нагрузке:

кН/м

то есть условие выполняется с запасом.

Следовательно, (как и отмечалось ранее) при расчете статически неопределимых систем по методу разрушающих нагрузок можно либо сэкономить материал, либо повысить расчетную нагрузку, при равных коэффициентах запаса прочности несущей способности и по разрушающей нагрузке.