4.4. Экспериментальное изучение свойств материалов при растяжении-сжатии

Для решения задач расчета и проектирования сооружений необходимо иметь данные о физико-механических характеристиках используемых материалов. В связи с этим разработаны разнообразные методики испытаний образцов, элементов моделей и натурных конструкций при действии различных видов нагрузок, без учета и с учетом факторов времени и температуры испытаний. Основным видом экспериментального исследования свойств материалов является испытание специально изготовленных образцов при растяжении-сжатии. Испытания регламентированы государственным стандартом (ГОСТ), что позволяет не только определять основные прочностные и деформационные характеристики материалов, но и проводить обоснованное сравнение различных конструкционных материалов по наиболее важным характеристикам их деформирования.

Испытания образцов материалов проводят на специальных испытательных машинах (прессы, разрывные и универсальные машины), с записью диаграммы испытаний.

Современные испытательные машины снабжены, как правило, электронными диспетчерскими устройствами, позволяющими варьировать программу испытаний. Они имеют выход на ЭВМ и снабжены программами обработки сигналов отклика при испытаниях.

Для испытаний на растяжение используют, в основном, образцы круглого поперечного сечения, форма которых показана на рис. 4.9, а. Они имеют утолщенные места для захвата образца и регламентированное ГОСТ отношение начальной рабочей длины и начального диаметра образца . Для испытаний на сжатие изготавливают образцы в виде кругового цилиндра (рис. 4.9, б; ) либо куба (рис. 4.9, в).

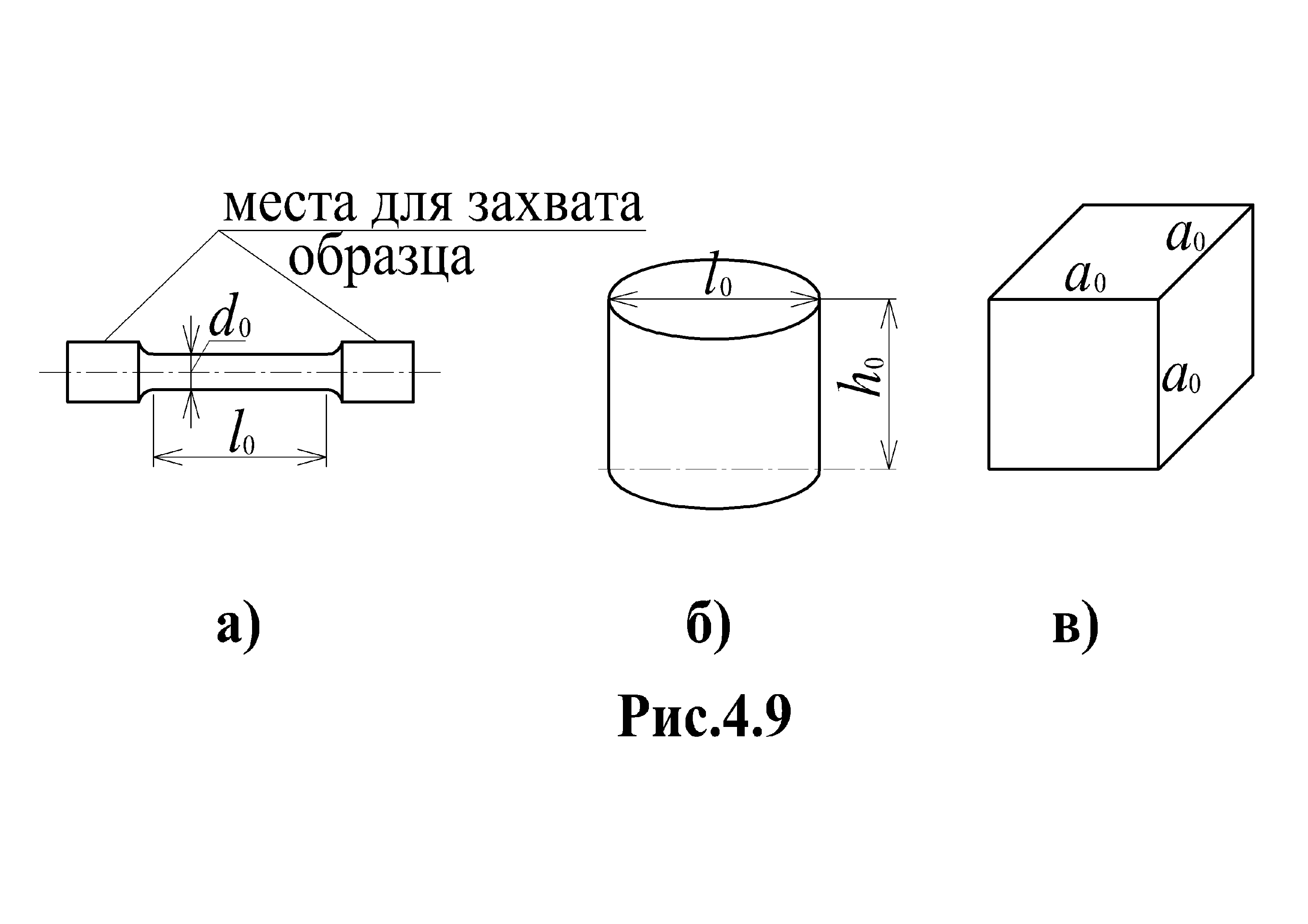
а) б) в)

Рис. 4.9

4.4.1. Диаграммы растяжения и сжатия пластичных материалов

Пластичными считаются материалы, которые до разрушения испытывают значительные необратимые (остаточные) деформации. К подобным материалам относятся стали, в частности, широко распространенная в строительной практике низкоуглеродистая сталь Ст3 (содержание углерода 0,09…0,25 % от объема), алюминий, медь, сплавы на основе перечисленных материалов и др.

На рис. 4.10 представлена диаграмма растяжения низкоуглеродистой стали Ст3 в осях F– . Участки, выделенные на диаграмме (см. рис. 4.10), соответствуют различным стадиям работы стали Ст3:

Рис. 4.10

ОА – участок пропорциональности ( ; сохраняется прямая пропорциональная зависимость между нагрузкой и деформацией образца);

ОАВ – участок упругости ( , деформация образца является упругой);

СD – площадка текучести ( ; интенсивно развиваются пластические деформации практически без увеличения нагрузки);

ВСD – участок общей текучести;

DЕ – участок упрочнения ( ; пластические деформации образца растут; одновременно возрастает сопротивление пластическому деформированию);

ЕK – участок прогрессирующего разрушения (местной текучести) ( появляется и начинает интенсивно развиваться так называемая «шейка», в зоне которой происходят интенсивные пластические деформации сдвига при снижении нагрузки).

Использование полученных в результате испытаний предельных значений нагрузки , , , неудобно, так как эти значения зависят от размеров испытуемого образца. Поэтому для характеристики прочностных свойств материалов используют значения условных напряжений

,

где – площадь поперечного сечения недеформированного образца.

Соответствующие предельные значения носят следующие названия:

– предел пропорциональности (для Ст3 МПа);

– предел упругости (для Ст3 МПа);

– предел текучести (для Ст3 МПа);

– временное сопротивление (для Ст3 МПа).

Кроме характеристик прочности, весьма важными для описания свойств пластичных материалов являются характеристики пластичности. Общая деформация образца в момент перед разрушением (см. рис. 4.10) равна , где – упругая часть деформации; – остаточная часть деформации.

Величина называется относительным остаточным удлинением (задается в процентах от первоначальной длины). Аналогично, величина называется относительным остаточным сужением (ΔА_ост – уменьшение площади поперечного сечения образца в «шейке» после разрыва; – первоначальная площадь сечения образца). Для Ст3 , Если по аналогии с условными напряжениями ввести условные деформации , то диаграмму при растяжении-сжатии можно преобразовать в условную диаграмму . Диаграммы для Ст3 при растяжении и сжатии показаны на рис. 4.11.

Согласно данным экспериментов, диаграмма сжатия Ст3 (и других сталей) до площадки текучести почти зеркально повторяет диаграмму растяжения. Поэтому прочностные пределы , при растяжении и сжатии сталей принимаются одинаковыми. Так как разрушить пластичный образец при сжатии не удается (он сплющивается), то выявить предел при сжатии стали также не удается, и в расчетах он условно принимается равным соответствующему пределу при растяжении.

На рис. 4.11 штрихами показана истинная диаграмма в «шейке» при растяжении. Как следует из приведенных диаграмм, разница между истинными и условными величинами , становится очень значительной на участке ЕK, причем по отношению к напряжениям эта разница становиться принципиальной: процесс разрушения происходит не с убыванием, а с нарастанием напряжений в «шейке».



Рис. 4.11

Кроме указанных прочностных пределов, по диаграммам , могут быть вычислены другие характеристики деформирования образцов и материалов. В частности: площадь диаграммы – работа, затраченная на разрушение образца; площадь диаграммы – условная удельная работа, затраченная на разрушение материала образца; – модуль упругости материала образца.

Рис. 4.12

Диаграммы растяжения-сжатия большинства пластичных конструкционных материалов (например, представленные на рис. 4.12 диаграммы растяжения легированной стали и алюминия) не имеют площадки текучести. Для таких материалов условный предел текучести принимается по величине остаточной деформации (точка N). Проводя из точки N линии, параллельные линиям пропорциональности OA, OA₂, получим точки D₁, D₂ на диаграммах , соответствующие , и величины , условных пределов текучести для заданных материалов 1, 2 (индекс 0,2 – величина остаточной деформации в процентах).