4.1. Определение напряжений в поперечных сечениях

Если на боковую поверхность стержня нанести линии, перпендикулярные продольной оси (т.е. принадлежащие поперечным сечениям), то при деформировании стержня эти линии, как правило, остаются близкими к перпендикулярным продольной оси. Это позволяет при определении напряжений использовать гипотезу плоских сечений (Я. Бернулли): сечения стержня, плоские и перпендикулярные продольной оси до деформации (поперечные сечения), остаются таковыми же в процессе деформации, перемещаясь параллельно самим себе.

Вырежем из стержня в районе произвольного сечения элементарный участок длиной dx (рис. 4.2). Будем полагать, что верхнее сечение условно неподвижно и силы внутреннего взаимодействия в нем суммированы к продольной силе N(x).

Из условия статики получим

, (4.1)

г де – искомая зависимость для нормальных напряжений.

Для выявления функции рас­смотрим геометрическую и физическую стороны задачи.

И

Рис. 4.2

з принятой схемы деформирования выделенного элемента стер­жня следует, что продольная деформация в точках поперечного сечения

, (4.2)

т.е. не зависит от координат y, z (постоянна в поперечном сечении).

При рассмотрении физической стороны задачи будем полагать, что продольные волокна не взаимодействуют в поперечных направлениях, то есть . Отсюда следует, что продольные волокна находятся в линейном напряженном состоянии. Полагая, что справедлив закон Гука и закон линейного температурного деформирования, получим:

, (4.3)

где функции, определяющие модуль упругости, коэффициент температурной деформации и изменение температуры в рассматриваемой точке объема.

Полагая в данном курсе, что величины , (одинаковы во всех точках сечения), получим

, (4.4)

т.е. нормальные напряжения равномерно распределяются по площади поперечного сечения.

Подставляем (4.4) в (4.1):

Таким образом, при введенных упрощающих гипотезах формула для нормальных напряжений в произвольном поперечном сечении стержня имеет вид:

(4.5)

где N(x) – продольная сила в рассматриваемом сечении;

A(x) – площадь рассматриваемого сечения.

Рассмотрим пример расчета стержня ступенчатого поперечного сечения при действии силовой нагрузки (рис. 4.3, а).

Дано:A₁ = 0,02м²; A₂ = 0,01 м².

Требуется: определить усилия и напряжения в поперечных сечениях стержня.

Опуская этап определения R₀ = 260 кН, приведем выражения для продольных сил на участках 1, 2:

(кН);

(кН) .

Учитывая (4.5), получим следующие значения нормальных напряжений в поперечных сечениях стержня на участках.

а) б) в) г)

Рис. 4.3

Участок 1, ; ;

, кН/м² = МПа;

, кН/м² = МПа.

Участок 2, : кН/м² = МПа = const.

Эпюры N, в поперечных сечениях стержня представлены на рис. 4.3, б, в.

4.2. Определение деформаций и перемещений

Из ранее выведенного соотношения (4.4) следует, что продольные деформации равномерно распределяются в поперечном направлении:

. (4.6)

При , , Эп В рассмотренном выше примере при МПа для получения Эп достаточно умножить ординаты Эп на 10^–4.

Рассмотрим прямой стержень, нагруженный продольной нагрузкой и состоящий из n участков (рис. 4.4).

Под участком i, i = 1,…, n, будем, в данном случае, понимать такую протяженность стержня, на которой функция не меняется. Используя соотношение (4.2), получим величину абсолютной деформации элементарной части стержня (рис. 4.2) на участке i:

. (4.7)

Рис. 4.4

Так как

,

то . (4.8)

Величина называется жесткостью стержня при растяжении (сжатии) на участке i. Суммируя деформации элементарных частей стержня на участке i, получим:

, (4.9)

где – координаты начала и конца участка i в выбранной системе координат. Суммируя абсолютные деформации участков, получим полную абсолютную деформацию (удлинение или укорочение) всего стержня при действии силовых нагрузок:

. (4.10)

Введем в рассмотрение функцию продольных перемещений сечений на участке i. Нетрудно заметить, что продольное перемещение сечения складывается из перемещения стержня как жесткого диска (перемещения начального сечения) и абсолютной деформации части стержня, заключенной между начальным и рассматриваемым сечениями. Для произвольного сечения на участке i

(4.11)

При жестком (неподатливом) закреплении начального сечения (рис. 4.4) u₀ = 0. В случае, когда начальное сечение закреплено линейно-податливой связью (опорой),

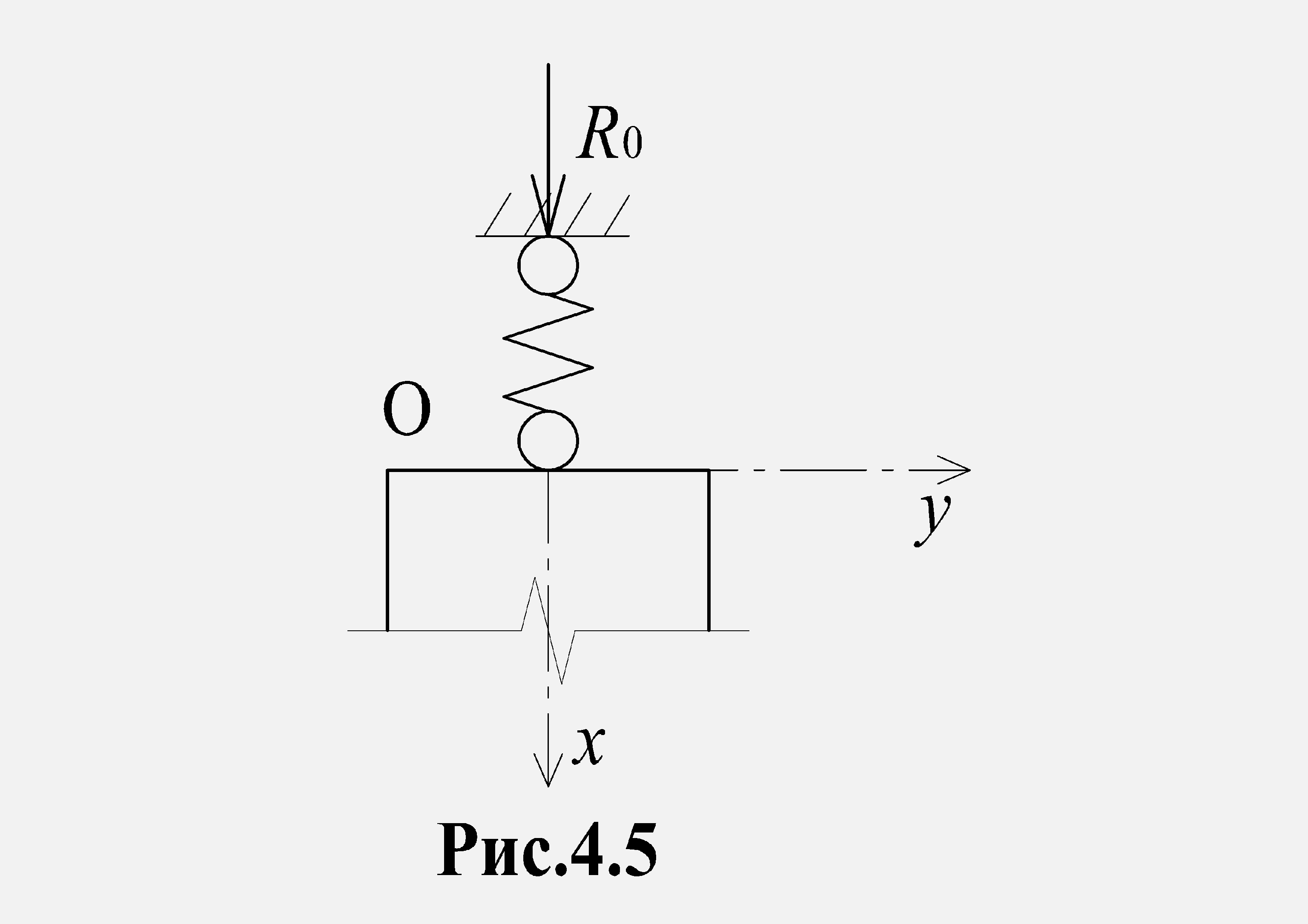, (4.12)

где R₀ – опорная реакция, k₀ (кН/м) – жесткость опоры, (м/кН) – податливость опоры.

В том случае, если , , i = 1,…, n (равномерное температурное воздействие на участках),

(4.13)

где .

При = 0, i = 1,…, n (температурное воздействие отсутствует), в выражениях (4.6)–(4.11) отсутствуют члены, зависящие от изменения температуры материалов на участках.

Продолжая пример расчета, рассмотренный выше (рис. 4.3), найдем абсолютную деформацию стержня и построим эпюру продольных перемещений сечений (рис. 4.3, г) при МПа = = 10⁷ кН/м²:

;