3.11. Удельная потенциальная энергия упругой деформации и ее составные части

Одним из основных методов решения задач механики деформируемого твердого тела является энергетический метод, основанный на анализе свойств функционалов энергии систем.

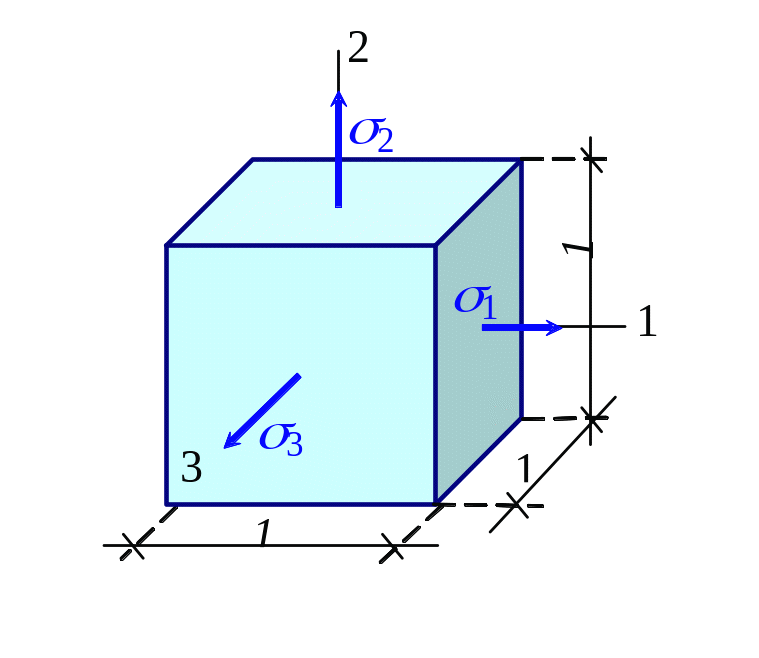
Рис. 3.16

Для определения удельной потенциальной энергии, накапливаемой изотропным материалом при линейно упругом деформировании, вырежем главными площадками из тела в окрестности рассматриваемой точки единичный объем (рис. 3.16).

Используя (3.35), получим величины главных деформаций:

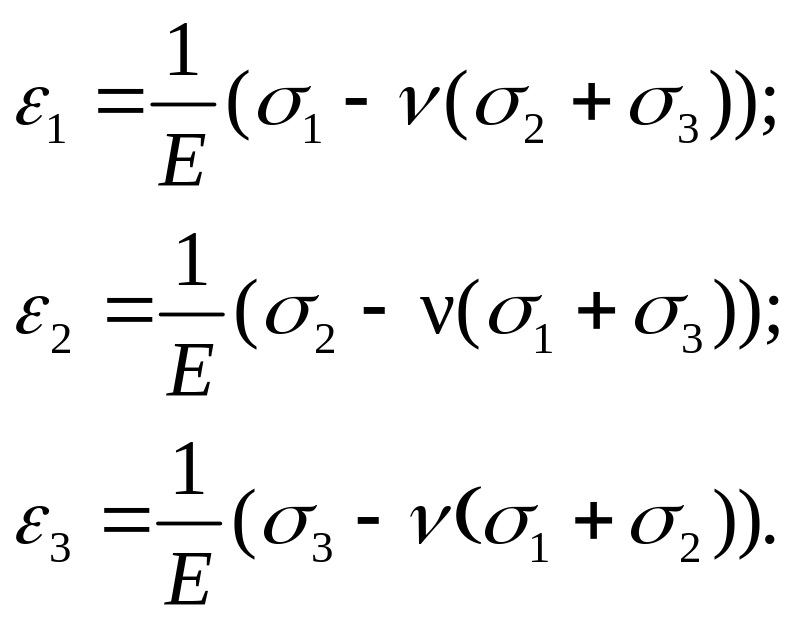(3.37)

Так как площади граней выделенного объема равны единицам, величины равны величинам равнодействующих сил внутреннего взаимодействия частиц на гранях и по отношению к выделенному элементу являются внешними силами. По той же причине перемещения вдоль равны . Энергия, накапливаемая в единичном объеме при статическом деформировании, равна работе внешних сил (без учета потерь), т.е.

. (3.38)

Подставляя (3.37) в (3.38), получим выражение для полной удельной потенциальной энергии упругой деформации изотропного тела:

(3.39)

Полную удельную потенциальную энергию упругой деформации можно представить в виде суммы

(3.40)

где – части, связанные с изменением объема и формы тела. Согласно (3.27), (3.37) объемная деформация в главной системе координат равна

, , (3.41)

где - модуль объемной упругости.

Для выделения части энергии, связанной с изменением объема, рассмотрим вспомогательное состояние, когда главные напряжения по граням выделенного объема равны среднему напряжению . В таком случае изменяется только объем элемента, а форма его не меняется. Это изменение для элемента единичного объема равно объемной деформации , т.е. совпадает с изменением объема элемента в заданном состоянии. Следовательно, полная удельная потенциальная энергия упругой деформации для вспомогательного состояния равна в заданном состоянии, т.е.

(3.42)

Часть удельной потенциальной энергии, связанная с изменением формы, может быть найдена из выражения

(3.43)

Подставляя (3.39), (3.42) в (3.43), после преобразований получим

(3.44)

4. Центральное растяжение-сжатие стержней

Под центральным растяжением-сжатием понимают сопротивление прямого стержня действию внешних нагрузок, направленных вдоль продольной оси стержня.

Н

Рис. 4.1

а рис. 4.1. показана расчетная схема прямого стержня, нагруженного продольными силовыми нагрузками. Стержень состоит из трех участков, причем на участках 1 и 2 площади поперечных сечений А₁ и А₂ и интенсивности распределенных нагрузок q₁ и q₂ постоянны, а на участке 3 A₃(x), q₃(x) – переменные величины. Стержень может быть выполнен из одного или нескольких материалов.

Воспользовавшись методом сечений, нетрудно показать, что в данном случае силы внутреннего взаимодействия в произвольном поперечном сечении суммируются только к продольной силе N(x), а остальные внутренние усилия тождественно равны нулю.