3.9. Закон Гука для линейного напряженного состояния и чистого сдвига. Поперечная деформация. Коэффициент Пуассона

Опыты, проводимые в XVII веке Р. Гуком по изучению деформирования стальной проволоки, позволили ему выявить прямо пропорциональную зависимость удлинения стержня от величины растягивающей силы. Однако понадобилось более ста лет, чтобы ввести понятия о напряжениях и деформациях и сформулировать закон линейного деформирования в виде

(3.30)

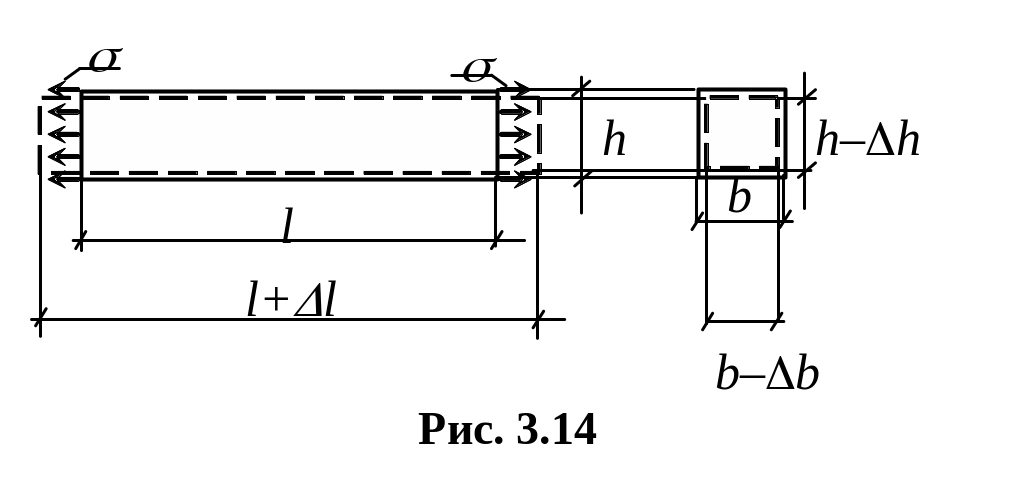
где – нормальное напряжение вдоль продольной оси стержня, – продольная деформация (рис. 3.14), – модуль упругости материала в рассматриваемом направлении. Зависимость (3.30) называется законом Гука для линейного напряженного состояния. Так как – величина безразмерная, модуль упругости имеет единицы измерения, совпадающие с единицами измерения напряжений.

Анализ деформирования стержня при растяжении позволяет заметить, что наряду с продольными изменяются и поперечные размеры образца (см. рис. 3.14). Величина (или ) называется поперечной деформацией, причем для изотропного материала .

Безразмерная величина называется коэффициентом Пуассона. Она является одной из постоянных упругости. С использованием коэффициента Пуассона получим:

. (3.31)

Изотропный материал характеризуется одним модулем упругости, одним коэффициентом Пуассона. Для анизотропного материала число соответствующих упругих постоянных больше единицы.

Проводя опыты при чистом сдвиге, аналогично опытам Р. Гука (рис. 3.15), получим зависимость, аналогичную (3.28):

, (3.32)

где – угол сдвига, – касательное напряжение, – модуль сдвига (модуль упругости второго рода). Зависимость (3.32) называется законом Гука при сдвиге для тела, выполненного из изотропного материала.

Рис. 3.15

3.10. Обобщенный закон Гука

Рассмотрим элемент объема (рис. 3.1, б), напряжения на гранях которого составляют полный тензор напряжений . В пределах линейно упругих деформаций компоненты напряженного и деформированного состояний связаны зависимостями, которые носят название обобщенного закона Гука. В самом общем случае эти зависимости можно записать в виде линейного преобразования

(3.33)

Соотношения (3.33) удобно представить в виде

, (3.34)

где – векторы деформаций и напряжений в координатных направлениях, – матрица жесткости материала в выбранной системе координат.

Сформулируем более детально обобщенный закон Гука для изотропного тела. Будем при этом полагать, что справедлив принцип суперпозиции и линейные и угловые деформации взаимно не связаны. Кроме того, будем полагать, что сдвиги в ортогональных плоскостях также не влияют друг на друга.

Используя принятые положения, найдем линейную деформацию вдоль оси . Она будет складываться из трех частей: . Величина – продольная деформация вдоль оси , связанная с , а величины , – поперечные деформации вдоль оси , связанные с . Аналогичным образом определяются составляющие линейных деформаций . Таким образом, с учетом суперпозиции получим:

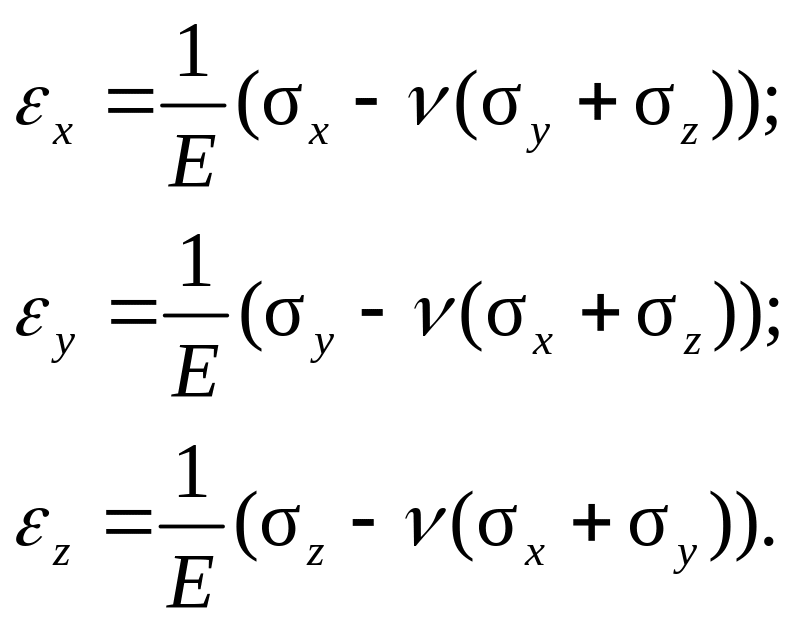(3.35)

С учетом принятых положений, для определения угловых деформаций достаточно воспользоваться законом Гука при чистых сдвигах в координатных плоскостях, т.е.

(3.36)

Зависимости (3.35), (3.36) носят название обобщенного закона Гука для изотропного тела.