
- •Содержание
- •1. Основные понятия, гипотезы и принципы, используемые в сопротивлении материалов 9
- •2. Определение внутренних усилий методом сечений 17
- •3. Теория напряженно-деформированного состояния материала в точке 34
- •4. Центральное растяжение-сжатие стержней 63
- •5. Критерии прочности и пластичности. Теории прочности 101
- •6. Геометрические характеристики плоских сечений 114
- •7. Кручение прямых стержней 130
- •Введение
- •1. Основные понятия, гипотезы и принципы, используемые в сопротивлении материалов
- •1.1. Расчетная схема сооружения
- •1.2. Типы связей (опор)
- •1.3. Классификация нагрузок
- •1.4. Деформации. Внутренние силы
- •1.5. Понятие о стержне (брусе). Основные виды деформации стержня
- •1.6. Гипотезы о характере деформирования и свойствах материалов. Основные упрощающие принципы
- •2. Определение внутренних усилий методом сечений
- •2.1. Идея метода сечений. Напряжения и внутренние усилия в сечениях
- •2.2. Внутренние усилия в поперечных сечениях стержня. Правила знаков
- •2.3. Понятие об эпюрах внутренних усилий в стержнях
- •2.4. Примеры построения эпюр внутренних усилий в стержнях
- •3. Теория напряженно-деформированного состояния материала в точке
- •3.1. Понятие о напряженном состоянии материала в точке. Тензор напряжений
- •3.2. Напряжения на наклонной площадке
- •3.3. Главные площадки и главные напряжения. Инварианты напряженного состояния
- •3.4. Виды напряженных состояний
- •3.5. Линейное напряженное состояние. Экстремальные касательные напряжения
- •3.6. Плоское напряженное состояние. Круги напряжений
- •3.7. Перемещения точек при деформировании материала. Линейные угловые и объемная деформации. Тензор деформаций
- •3.8. Аналогия в описании деформированного и напряженного состояний материала в точке. Главные деформации
- •3.9. Закон Гука для линейного напряженного состояния и чистого сдвига. Поперечная деформация. Коэффициент Пуассона
- •3.10. Обобщенный закон Гука
- •3.11. Удельная потенциальная энергия упругой деформации и ее составные части
- •4. Центральное растяжение-сжатие стержней
- •4.1. Определение напряжений в поперечных сечениях
- •4.2. Определение деформаций и перемещений
- •4.3. Статически неопределимые системы при растяжении-сжатии и порядок их расчета
- •4.4. Экспериментальное изучение свойств материалов при растяжении-сжатии
- •4.4.1. Диаграммы растяжения и сжатия пластичных материалов
- •4.4.2. Наклеп. Понятие о ползучести материалов. Основные проявления ползучести
- •4.4.3. Диаграммы испытаний хрупких материалов
- •4.4.4. Влияние температуры и скорости испытаний на механические характеристики материалов
- •4.4.5. Нормативные и расчетные сопротивления материалов
- •4.5. Методы расчета конструкций
- •4.5.1. Расчет по допускаемым напряжениям
- •4.5.2. Расчет по предельным состояниям
- •4.5.3. Расчет по разрушающим предельным нагрузкам
- •4.6. Примеры решения поверочных и проектных задач при расчетах по предельным состояниям и разрушающим нагрузкам
- •5. Критерии прочности и пластичности. Теории прочности
- •5.1. Предельное состояние материала. Хрупкое и вязкое разрушение
- •5.2. Понятие о равноопасных напряженных состояниях. Эквивалентные напряжения
- •5.3. Критерии разрушения. Первая и вторая теории прочности
- •5.4. Критерии пластичности. Третья и четвертая теории прочности
- •5.5. Теория прочности Мора
- •5.6. Понятие о новых теориях прочности
- •5.6.1. Теория прочности Давиденкова – Фридмана
- •5.6.2. Объединенные теории прочности
- •6. Геометрические характеристики плоских сечений
- •6.1. Основные интегральные характеристики плоских сечений
- •6.2. Моменты инерции сечений простой формы
- •6.3. Формулы перехода при параллельном переносе и повороте осей
- •6.3.1. Параллельный перенос осей
- •6.3.2. Поворот осей
- •6.4. Главные оси инерции и главные моменты инерции. Радиусы инерции
- •6.5. Пример расчета
- •7. Кручение прямых стержней
- •7.1. Определение усилий в поперечных сечениях
- •7.2. Кручение стержней круглого и кольцевого сечений
- •7.2.1. Определение напряжений в поперечных сечениях. Расчет на прочность
- •7.2.2. Определение углов закручивания сечений. Расчет по деформациям (на жесткость)
- •7.2.3. Расчет по разрушающей (предельной) нагрузке
- •7.3. Кручение стержней прямоугольного сечения
- •7.3.1. Понятие о депланации сечений
- •7.3.2. Свободное кручение стержней прямоугольного сечения. Расчеты на прочность и жесткость
- •7.4. Свободное кручение стержней, сечение которых составлено из прямоугольников
- •Профильные линии
- •7.4.1. Кручение стержней открытого профиля
- •7.4.2. Кручение стержней замкнутого профиля
- •7.5. Статически неопределимые задачи при кручении
- •7.5.1. Учет линейно упругой податливости опорных связей
- •7.5.2. Примеры расчетов статически неопределимой системы различными методами
- •Расчет по несущей способности (по прочности)
- •Расчет по предельной нагрузке
- •Библиографический список
3.7. Перемещения точек при деформировании материала. Линейные угловые и объемная деформации. Тензор деформаций
В процессе деформирования тела под нагрузкой его точки перемещаются в пространстве (рис. 3.11).
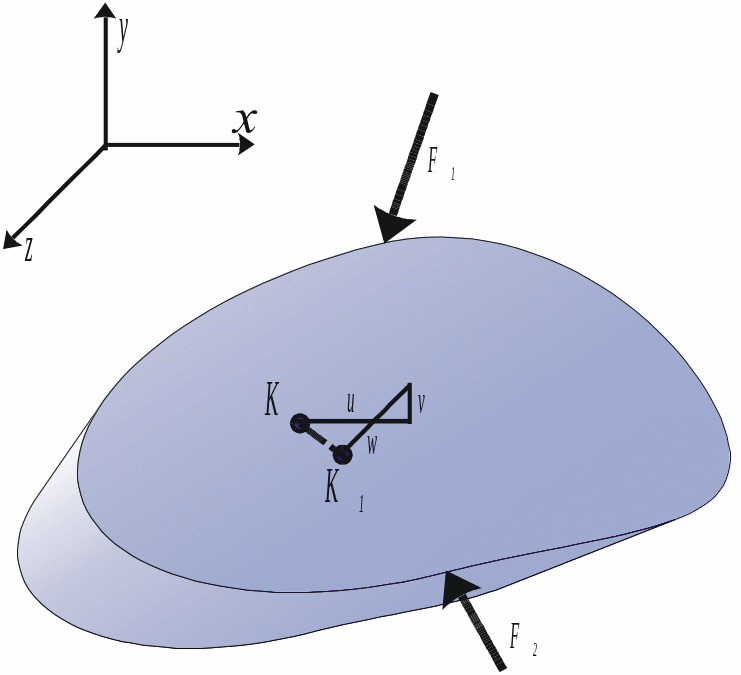
Рис. 3.11
Полное
перемещение KK1
исследуемой точки K
можно представить как геометрическую
сумму ее перемещений в координатных
направлениях. Составляющие
![]() в декартовой системе координат показаны
на рис. 3.11. Величины
являются функциями координат точек:
в декартовой системе координат показаны
на рис. 3.11. Величины
являются функциями координат точек:
![]()

Рис. 3.12
Д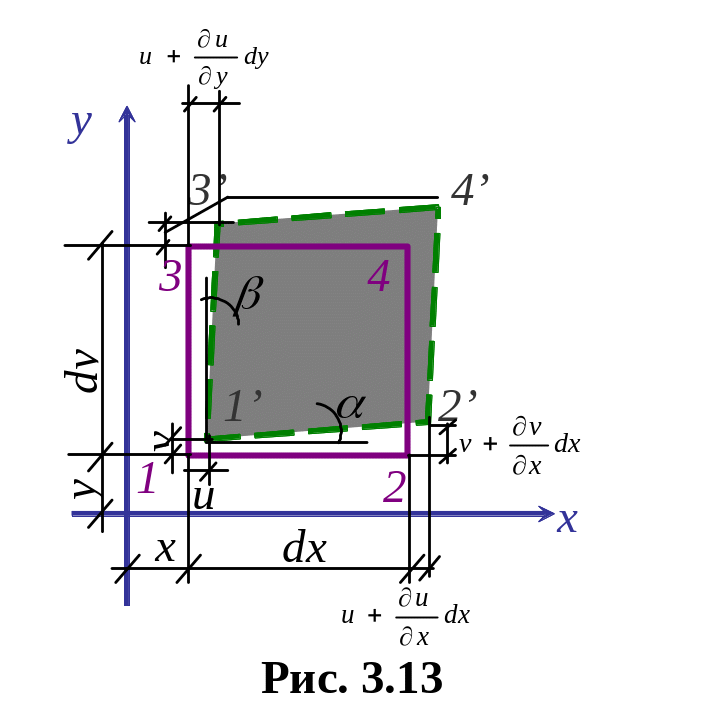 ля
характеристики деформированного
состояния тела в окрестности исследуемой
точки K рассмотрим
элементарный параллелепипед, содержащий
точку K (рис. 3.12).
Деформированный параллелепипед показан
на рис. 3.12 штриховыми линиями, причем в
силу малости объема можно полагать, что
его грани остались плоскими.
ля
характеристики деформированного
состояния тела в окрестности исследуемой
точки K рассмотрим
элементарный параллелепипед, содержащий
точку K (рис. 3.12).
Деформированный параллелепипед показан
на рис. 3.12 штриховыми линиями, причем в
силу малости объема можно полагать, что
его грани остались плоскими.
П
![]()
![]() ,
учитывается только линейная часть
приращений перемещений.
,
учитывается только линейная часть
приращений перемещений.
Согласно
рис. 3.13 изменения размеров выделенного
элемента вдоль осей
![]() равны
равны
![]()
![]() Аналогично
Аналогично
![]()
О тносительные
величины
тносительные
величины
![]() (3.25)
(3.25)
называют
линейными деформациями вдоль осей
![]() в точке K.
в точке K.
Изменения
первоначально прямых углов между ребрами
выделенного параллелепипеда называются
угловыми деформациями (деформациями
сдвига). В частности, сдвиг
![]() между
ребрами, параллельными осям
равен сумме
между
ребрами, параллельными осям
равен сумме
![]() .
В силу малости углов
.
В силу малости углов
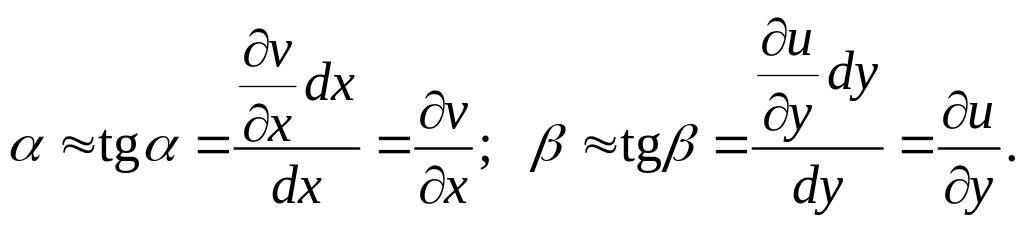 Таким образом, величины угловых деформаций
определяются соотношениями
Таким образом, величины угловых деформаций
определяются соотношениями
![]() (3.26)
(3.26)
Матрица
 называется тензором деформаций в
исследуемой точке K.
называется тензором деформаций в
исследуемой точке K.
Совокупность линейных и угловых деформаций для всевозможных направлений в окрестности исследуемой точки K называется деформированным состоянием в точке K.
Из
выражений (3.25) следует, что изменения
линейных размеров выделенного элемента
могут быть получены через линейные
деформации:
![]() .
Тогда объем деформированного элемента
равен
.
Тогда объем деформированного элемента
равен
![]() .
.
Относительная характеристика изменения объема выделенного элемента равна

Величина
![]() называется объемной деформацией
материала в точке. Так как обычно
называется объемной деформацией
материала в точке. Так как обычно
![]() ,
то, пренебрегая величинами второго и
третьего порядка малости, получим
,
то, пренебрегая величинами второго и
третьего порядка малости, получим
![]() .
(3.27)
.
(3.27)
3.8. Аналогия в описании деформированного и напряженного состояний материала в точке. Главные деформации
Анализ
деформированного состояния показывает,
что оно обладает свойствами, аналогичными
свойствам напряженного состояния. В
частности, нетрудно показать, что
линейные и угловая деформации в осях![]() ,
повернутых при вращении относительно
оси
,
повернутых при вращении относительно
оси
![]() к осям
под углом
,
определяются выражениями, аналогичными
(3.18), (3.19):
к осям
под углом
,
определяются выражениями, аналогичными
(3.18), (3.19):
 (3.28)
(3.28)
Этот факт является одним из проявлений так называемой статико-геометрической аналогии в механике деформируемого твердого тела.
По
аналогии с напряженным состоянием можно
утверждать, что в окрестности каждой
точки деформируемого тела можно выделить
три взаимно перпендикулярных направления,
сдвиги между которыми отсутствуют. Эти
направления называются главными.
В теле, выполненном из изотропного
материала, они совпадают с направлениями
главных напряжений. Линейные деформации
![]() в главных направлениях называются
главными деформациями, причем
в главных направлениях называются
главными деформациями, причем
![]() .
Величины главных деформаций являются
решением кубического уравнения (см.
3.11):
.
Величины главных деформаций являются
решением кубического уравнения (см.
3.11):
![]() (3.29)
(3.29)
где
![]()

– инварианты деформированного состояния. Деформированное состояние можно графически описать с помощью трех кругов деформаций, аналогичных кругам напряжений (см. рис. 3.9).
