4. Энергетическая скрытность при

НАЛИЧИИ ПОИСКА СИГНАЛА

4.1. Поиск сигнала по энергетическим характеристикам

Пусть искомый сигнал может излучаться на одной из частот , которые выбираются передатчиком с вероятностями , . Для его выявления необходимо провести двоичную поисковую процедуру и по энергетическим характеристикам установить присутствие сигнала на рабочей частоте .

Примеры алгоритмов поиска приведены на рис. 4.1. На рис. 4.1а показано дерево поиска алгоритма последовательного,

Рис. 4.1 а на рис. 4.1б – дихо-

томического поиска.

Двоичное измерение заключается в настройке энергетического приемника на выбранную группу рабочих частот и формировании решения о наличии или отсутствии сигнала в анализируемой полосе частот.

Принятое решение может быть правильным или ошибочным. Возможны два рода ошибок [1]. Ошибка первого рода (ложная тревога) возникает с вероятностью , если принимается решение о наличии сигнала при его фактическом отсутствии (всплеск шума воспринимается как сигнал). Ошибка второго рода (пропуск сигнала) возникает с вероятностью , если принято решение об отсутствии сигнала при его фактическом наличии (шум подавил сигнал).

Результаты поиска определяются решениями, полученными в коде каждого проведенного измерения.

48

4.2. Характеристики алгоритма последовательного

поиска с ошибками

Дерево последовательного поиска показано на рис. 4.2. В ходе первого измерения из всего множества частот выбирается первая рабочая частота и проверяется наличие на ней искомого сигнала. Если принято отрицательное решение, то проверяется вторая частота и так далее. При последнем измерении проверяется частота и при отрицательном результате принимается Рис. 4.2

решение о наличии сигнала на

частоте .

Допустим, что рабочая частота выбирается передатчиком равновероятно из множества ,

. (4.1)

Узкополосный энергетический приемник поочередно настраивается на выбранные рабочие частоты и проверяет наличие на них искомого сигнала.

Рассчитаем апостериорные распределения вероятностей после первого измерения, показанного на рис. 4.3.. Пусть принято решение об обнаружении сигнала на частоте . Апостериорная вероятность нахождения сигнала на частоте равна Рис. 4.3

49

. (4.2)

Условная вероятность принятия решения о наличии сигнала на частоте при условии, что он там фактически присутствует, равна . Решение принимается, если сигнал присутствует на частоте с вероятностью и он не пропущен или если сигнал отсутствует на частоте с вероятностью , но произошла ложная тревога. Тогда получим

(4.3)

и из (4.2)

. (4.4)

Для остальных частот , , по формуле Байеса запишем

. (4.5)

Условная вероятность принятия решения о наличии сигнала на частоте при условии, что он там отсутствует, равна , тогда с учетом (4.3) при получим

. (4.6)

50

Введем обозначение

(4.7)

( - номер частоты, - номер измерения), тогда для всех получим

. (4.8)

Пусть принято решение об отсутствии сигнала на частоте , тогда

. (4.9)

Аналогично предыдущему можно показать, что

, (4.10)

(4.11)

Проведите расчет самостоятельно.

На рис. 4.4 приведены апостериорные распределения вероятностей (4.8) (рис. 4.4а) и (4.10) (рис. 4.4б) для решений о наличии и отсутствии сигнала на частоте соответственно при и . Вероятность (4.4) определяет вероятность правильного решения о наличии сигнала на частоте ,

51

. (4.12)

Рис. 4.4

Фрагмент дерева поиска после второго измерения показан на рис. 4.5. После первого измерения при обнаружении сигнала на частоте (решение ) поиск заканчивается. Второе измерение возникает при решении об отсутствии сигнала на частоте ( ) и для него априорным распределением вероятностей состояния передатчика является

Рис. 4.5 апостериорное распределение

вероятностей вида (4.10). Тогда аналогично предыдущему получим

, (4.13)

, (4.14)

52

. (4.15)

В результате можно записать общие выражения для апостериорных вероятностей после -го измерения, , в виде

, (4.16)

, (4.17)

. (4.18)

Эти зависимости показаны на рис. 4.6 при и . Программа расчетов в пакете программ MathCAD приведена на рис. 4.7. Напишите аналогичную программу в любой система программирования самостоятельно.

Рис. 4.6

53

Рис. 4.7

54

Дерево поиска с указанием вероятностей перехода по его ветвям показано на рис. 4.8.

Рис. 4.8

Вероятности , , обнаружения сигнала в подмножествах частот и его выявления на частоте определяются выражением (4.18), их зависимости от показаны на рис. 4.9. При отсутствии помех для вероятности обнаружения сигнала на частоте получим , а для со- Рис. 4.9

55

ответственно , их зависимости от показаны на рис. 4.8 пунктиром.

Для расчета вероятностей решений о наличии сигнала на частоте ( ) целесообразно изобразить дерево поиска с вероятностями перехода к соответствующим состояниям при заданном истинном значении рабочей частоты , показанное на рис. 4.10. Событие обведено кружком, финальный узел отмечен зачерненным кружком

Рис. 4.10

56

Вероятности решений получаются при движении по дереву поиска на рис. 4.10 перемножением соответствующих вероятностей. Нетрудно показать, что условные вероятности принятия решения о наличии сигнала на частоте ( ) при фактическом наличии сигнала на частоте можно записать в виде

(4.19)

Получите эти выражения самостоятельно.

Тогда безусловные вероятности окончательных решений равны

. (4.20)

Для равновероятного выбора рабочих частот с учетом [5] получим

(4.21)

57

а при соответственно

(4.22)

Распределение вероятностей решений показано на рис. 4.11 при , равных вероятностях ошибок и равновероятном выборе рабочих частот .

Рис. 4.11

Как видно, при малых вероятностях ошибок вероятности совпадают с . При высоких существенно повышаются вероятности выявления сигнала при первых измерениях в основном за счет ложных тревог.

На рис. 4.12 показаны зависимости при различных соотношениях между вероятностями ложной тревоги и пропуска сигнала: (сплошная линия), (широкий пунктир) и (узкий пунктир). Проанализируйте полученные результаты.

58

Рис. 4.12

Расчеты вероятностей можно провести и на основе дерева поиска на рис. 4.8, для которого

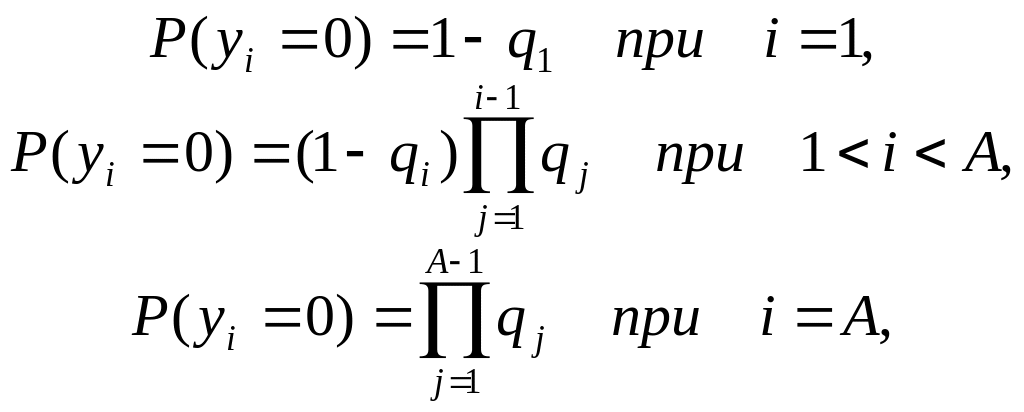(4.23)

а вероятности решений об отсутствии сигнала на частоте после -го измерения определяются из формул (4.18) и (4.17). Результаты расчетов по (4.22) и (4.23) совпадают, проверьте это самостоятельно.

4.3. Достоверность последовательного поиска

Принятые в результате поиска решения могут быть правильными или ошибочными. Для оценки достоверности результатов поиска можно воспользоваться вероятностями принятия решения о наличии сигнала на частоте при его фактическом присутствии на частоте

59

вида (4.19). Пример двумерной вероятностной диаграммы показан на рис. 4.13а.

Рис. 4.13

Достоверность поиска можно характеризовать минимальной вероятностью принятия после -го измерения решения о наличии сигнала на частоте при его фактическом присутствии на этой частоте, то есть, что принятое решение правильно. Из (4.19) получим

(4.24)

Пример зависимости от показан на рис. 4.13б. Как видно, эти вероятности падают с ростом номера измерения и их минимальное значение достигается при , если , или при , если . В результате получим

(4.25)

60

Из (4.25) следует, что вероятность ложной тревоги снижает достоверность обнаружения существенно сильнее, чем вероятность пропуска сигнала, поэтому при больших арсеналах целесообразно обеспечить условие за счет повышения порога принятия решения о наличии сигнала по сравнению с условием . Тогда окончательно получим выражение для достоверности поиска в виде

(4.26)

Зависимость от и при в виде трехмерной поверхности показана на рис. 4.14а. Как видно, повышение вероятности ложной тревоги снижает достоверность значительно быстрее, чем вероятности пропуска сигнала. С ростом арсенала частот это проявляется еще нагляднее.

Рис. 4.14

Если все же выполняется условие , то получим выражение

, (4.27)

61

в котором достоверность поиска не зависит от . Зависимости от из (4.27) при различных показаны на рис. 4.15. Сравните зависимости на рис 4.13а и 4.14.

Достоверность поиска можно также характеризовать средней веро-

Рис. 4.15 ятностью принятия реше-

ния о наличии сигнала на той частоте, на которой он фактически присутствует, то есть средней вероятностью принятия правильного решения. Проанализируйте достоинства и недостатки меры достоверности по сравнению с . Из (4.25) при равновероятном выборе рабочих частот получим [5]

(4.28)

Зависимость от и при в виде трехмерной поверхности показана на рис. 4.14б. Сравнивая диаграммы на рис. 4.14а и рис. 4.14б, можно убедиться в их подобии (можно отметить большую пологость поверхности ), поэтому в качестве меры достоверности поиска целесообразно выбрать величину согласно (4.26) или (4.27).

В качестве меры достоверности поиска можно использовать минимальную или среднюю вероятность нахождения

62

сигнала на частоте при условии, что принято решение о наличии сигнала на этой частоте. Это апостериорная вероятность , получаемая из (4.16) при и вычисляемая на основе рекуррентных соотношений (4.16) – (4.18), их трехмерная диаграмма показана на рис. 4.6. На рис. 4.16 показаны зависимости от для различных значений вероятностей ложной тревоги и пропуска сигнала при .

Рис. 4.16

Использование апостериорных вероятностей для оценки достоверности поиска приводит к громоздким выражениям и практически не удобно.

Таким образом в качестве меры достоверности последовательного поиска целесообразно принять величину вида (4.26).

Вероятность ложной тревоги (2.34) зависит от порога решающего правила (3.30) и объема выборки отсчетов, а вероятность пропуска сигнала - еще и от отношения сигнал/шум (3.37). Тогда для достоверности поиска из (4.26) получим

63

4.29)

Функцию можно максимизировать по величине порога , примеры соответствующих зависимостей показаны на рис. 4.17 при и (для удобства показаны величины ). Величиной отмечено значение при , соответствующее (4.27).

Рис. 4.17

64

Аналогичные зависимости при показаны на рис. 4.18.

Рис. 4.18

Проведенные расчеты показывают, что выбор оптимального порога в (4.26) приводит к повышению достоверности (уменьшению величины ). При малых арсеналах (рис. 4.17) эффективность такой оптимизации невелика и минимум незначительно отличается от величины , получаемой из (4.27) в предположении, что . При больших наблюдается значительное повышение достоверности последовательного поиска при оптимальном выборе порога, как показано на рис. 4.18.

Расчеты достоверности с оптимальным порогом требуют сложных вычислений, и в дальнейшем будем полагать, что достоверность поиска определяется величиной согласно (4.27) при условии

. (4.30)

Тогда вероятность ошибки равна

65

. (4.31)

Зависимость допустимой вероятности ошибки от требуемой достоверности поиска показана на рис. 4.19. Как видно, при высокой достоверности поиска и больших

Рис. 4.19 арсеналах предъявляя-

ются жесткие требования к величине допустимой вероятности ошибок.

4.4. Продолжительность двоичного измерения

Продолжительность двоичного измерения для энергетического приемника определяется требуемой вероятностью ошибки из соотношений (2.30) – (2.37) вида

, (4.32)

, (4.33)

, (4.34)

. (4.35)

С учетом (4.31) из (4.32) необходимое число отсчетов

66

можно найти из решения уравнения вида

. (4.36)

Текст программы приведен на рис. 4.20. В верхней части рис. 4.21 показаны зависимости от для различных и .

Рис. 4.19

Рис. 4.20

67

Продолжительность двоичного измерения в числе отсчетов сигнала при энергетическом обнаружении повышается с ростом арсенала частот и требуемой достоверности обнаружения . В значительно большей степени затраты на обнаружение увеличиваются при уменьшении отношения сигнал/шум .

В нижней части рис. 4.21 показаны аналогичные зависимости от при обнаружении детерминированного сигнала (подраздел 2.1). Из сравнения зависимостей на рис. 4.21 следует, что знание формы сигнала и его согласованная фильтрация многократно снижают затраты на его обнаружение. Например, для и при и энергетическом обнаружении необходимо , а при согласованной фильтрации детерминированного сигнала требуется всего отсчетов.

С другой стороны, для фиксированного значения и при энергетическом обнаружении требуется обеспечить отношение сигнал/шум , а при согласованной фильтрации достаточно иметь , то есть в 19 раз меньше.

На рис. 4.22 показаны зависимости от отношения сигнал/шум энергетического выигрыша ,

, (4.37)

в числе отсчетов при обнаружении детерминированного сигнала ( ) по сравнению с обнаружением стохастического сигнала ( ).

68

Рис. 4.22

Как видно, полная информация о форме сигнала особенно необходима при малых и высоких требованиях к достоверности обнаружения.

Продолжительность двоичного измерения в единицах времени определяется соотношением

, (4.38)

где - частота квантования сигнала в соответствии с теоремой Котельникова, - период квантования, - ширина спектра сигнала.

4.5. Расчет скрытности при последовательном поиске

с ошибками

По определению [4] алгоритмическая скрытность – это среднее число двоичных измерений, необходимое для выявления состояния объекта поиска (рабочей частоты радиопередатчика) с заданной достоверностью.

69

Расчет скрытности проводится следующим образом:

- при заданной достоверности поиска вычисляются требуемые значения вероятностей ошибок и ;

- при выбранном способе обработки сигнала определяется длительность (в числе отсчетов) двоичного измерения, необходимая для обеспечения требуемых вероятностей ошибок;

- при известных вероятностях ошибок вычисляется среднее число двоичных измерений и скрытность в числе отсчетов сигнала или в единицах времени.

Для алгоритма последовательного поиска с деревом вида рис. 4.9 получим

. (4.39)

Вероятности решений определяются из (4.21) и (4.22). Подставляя их в (4.39) и суммируя прогрессии вида

, ,

,

можно получить весьма громоздкое общее выражение для скрытности (попытайтесь проделать эти вычисления).

В частном случае при

(4.40)

получим

70

. (4.41)

Зависимости алгоритмической скрытности от вероятности ошибки (4.40) для различных арсеналов множества частот показаны на рис. 4.23а. На рис. 4.23б представлены зависимости от достоверности поиска (в масштабе ).

Рис. 4.23

71

С ростом вероятности ошибок среднее число измерений (алгоритмическая скрытность) падает по сравнению со значением для безошибочного поиска при равновероятном выборе частот [4], равным

(4.42)

(получите это соотношение самостоятельно). Это обусловлено увеличением вероятностей ошибочного раннего завершения поиска. Об этом свидетельствуют графики на рис. 4.23б. Там, где достоверность или , скрытность при наличии помех практически равна (4.42).

На практике приемлемые значения достоверности поиска должны лежать в пределах , то есть заведомо удовлетворять условию . Тогда скрытность в двоичных измерениях при последовательном поиске сигнала в шумовых в помехах определяется выражением

. (4.43)

Как было установлено ранее (рис. 4.20), продолжительность двоичного измерения существенно зависит от отношения сигнал/шум в измерительном приемнике , тогда скрытность сигнала в числе отсчетов (периодов квантования) равна

. (4.44)

Зависимости от показаны на рис. 4.24 сплошными линиями при энергетическом обнаружении стохастического сигнала и пунктирными при согласованной фильтрации детерминированного сигнала.

72

Рис. 4.24

Значения скрытности в числе отсчетов сигнала в (рис. 4.21) раз больше значений скрытности в двоичных измерениях на рис. 4.23а. Как видно, с ростом арсенала сигналов и требуемой достоверности поиска скрытность .многократно возрастает даже при обнаружении детерминированных сигналов.

Для стохастических сигналов значения энергетической скрытности велики даже при высоких отношениях сигнал/шум. Например, при , и для скрытности получим отсчетов, тогда для сигнала с шириной спектра 10 кГц период квантования равен мкс и энергетическая скрытность сигнала в единицах времени будет равна 1 с. При уменьшении до 1 энергетическая скрытность повышается на порядок, а при становится еще в 100 раз больше.

73

4.6. Кривая снятия неопределенности

В процессе поиска меняется неопределенность рабочей частоты сигнала. В -м измерении проверяется наличие или отсутствие сигнала на частоте . При обнаружении сигнала (принято решение ) поиск прекращается и полученное решение характеризуется апостериорным распределением вероятностей (рис. 4.4а) и остаточной неопределенностью множества рабочих частот , равной

. (4.45)

При отсутствии шума . Если сигнал не обнаружен, то поиск будет продолжен. Вероятности наличия сигнала на различных частотах равны апостериорным вероятностям , (рис. 4.4б), а энтропия множества рабочих частот равна

. (4.46)

Апостериорные вероятности определяются соотношениями (4.16) – (4.18), их трехмерные диаграммы показаны на рис. 4.6, а программа вычислений – на рис. 4.7. Средняя энтропия множества рабочих частот после -го измерения равна

. (4.47)

Зависимости условных , и

74

безусловной энтропий от номера проведенного двоичного измерения показаны на рис. 4.25 при и равных вероятностях ошибок при которых . Пунктиром показаны зависимости при безошибочном поиске ( ), вычисляемые по формулам

, (4.48)

(4.49)

(получите их самостоятельно).

Рис. 4.25

Условная энтропия характеризует остаточную неопределенность по завершении поиска при обнаружении сигнала при -м измерении на частоте . При отсутствии помех она равна нулю.

75