3. Энергетическая скрытность при

ОТСУТСТВИИ ПОИСКА СИГНАЛА

3.1. Методы оценки скрытности при отсутствии поиска

Допустим, что выявляемый сигнал не меняет своих параметров и известны его частота настройки, ширина спектра и энергетические характеристики сигнала и шума. Тогда разведка сигнала заключается в его обнаружении энергетическими методами без использования поисковых процедур [4].

При отсутствии помех (шума) любой сигнал обнаруживается практически мгновенно при появлении первого ненулевого отсчета и его скрытность равна нулю.

При наличии помех для обнаружения сигнала с заданной достоверностью требуется вполне определенное время (число отсчетов ). Если достоверность не задана, то обработку отсчетов сигнала можно не производить, а использовать угадывание его наличия, при этом затраты на обнаружение отсутствуют и скрытность вновь оказывается равной нулю. Таким образом при отсутствии сменности рабочих параметров сигнала их поиск отсутствует и можно говорить только об их скрытности в помехах (шумах).

В этом случае скрытность [4] определяется затратами времени (отсчетов ), необходимыми для выявления сигнала с заданной достоверностью.

Скрытность сигнала зависит от наличия информации о его форме (возможности вести когерентную или некогерентную его обработку). Если информация о форме сигнала отсутствует, то скрытность определяется только энергетикой сигнала и помехи. В этом случае удобной моделью является стохастический сигнал при оптимальном энергетическом обнаружении а его скрытность будем называть энергетической.

Описание узкополосных и широкополосных сигналов различных типов приведено в приложении 1.

36

3.2. Длительность обнаружения широкополосного

сигнала

Широкополосный сигнал (ШПС) занимает полосу частот f_с, равную ширине спектра шума f_ш, тогда обозначим

. (3.1)

При мощности сигнала его спектральная плотность согласно (2.74) равна

. (3.2)

Вероятности ложной тревоги и пропуска сигнала при больших объемах выборки N определяется выражениями (2.34) и (2.35), которые можно записать в виде

, (3.3)

, (3.4)

где отношение сигнал/шум h² равно

, (3.5)

 определяется из (2.31), а F(x) - интеграл Лапласа (2.36).

37

При заданных вероятности ложной тревоги и числе отсчетов сигнала из (3.3) можно найти обратную функцию

, (3.6)

определяющую порог решающего правила (2.31). Подставляя его в (3.4), получим зависимость вероятности пропуска сигнала от объема выборки при заданных вероятности ложной тревоги и отношении сигнал/шум (критерий Неймана - Пирсона). Из (3.4) можно найти обратную функцию

, (3.7)

определяющую необходимый объем выборки, при котором обеспечиваются заданные вероятности ошибок.

При малых N<100 функции (3.6) и (3.7) необходимо определять из выражений (3.32) и (3.33) соответственно.

На рис.3.1 показана зависимость N₁ (в логарифмическом масштабе) от (в децибелах) при и . В области <1 графики практически прямолинейны и после преобразования логарифмических масштабов могут аппроксимироваться, например, выражением

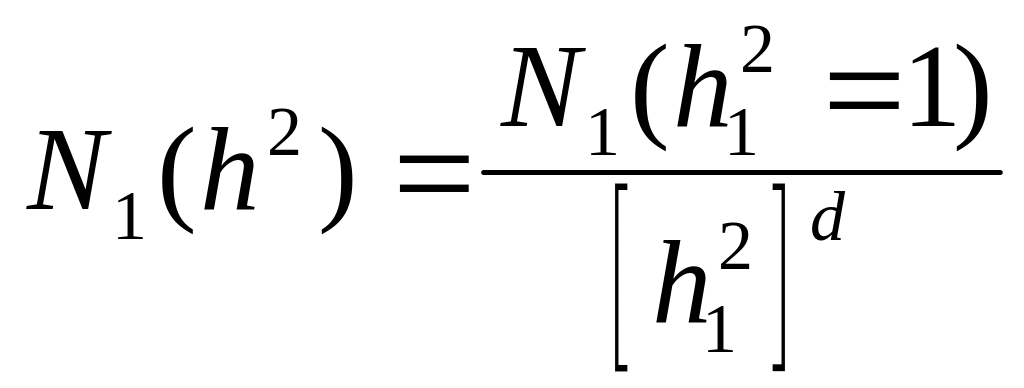. (3.8)

При из (3.7) получим и , тогда из (3.8) следует . То же значение параметра получается и при , когда и . Таким обра-

38

зом, аппроксимация (3.8) оказывается вполне удовлетворительной в области h₁²<1.

Рис. 3.1

Согласно (2.72) время обнаружения ШПС t_обн1 равно

. (3.9)

Например, при и (-30 дБ) получим N₁=7.64710⁷, тогда при МГц из (3.9) с.

Как видно, энергетическое обнаружение ШПС при малых отношениях сигнал/шум требует значительных временных затрат. При этом необходимо учитывать, что для реализации алгоритма обнаружения, например (2.31), в приемнике необходимо точно знать (измерять) уровни сигнала и шума. Если , то и ее измерение на фоне шумов весьма затруднительно.

39

3.3. Длительность обнаружения узкополосного сигнала

Узкополосный сигнал в виде нормального случайного процесса с нулевым средним и дисперсией (мощностью) занимает полосу частот .

Отношение сигнал/шум определяется выражением

, (3.10)

где - спектральная плотность мощности белого шума. Для узкополосного сигнала отношение сигнал/шум .

Увеличение отношения сигнал/шум приведет к снижению требуемого для обнаружения объема выборки , который может быть определен из (3.7).

Выражения (2.34) и (2.35) позволяют проводить расчеты при >200, так как происходит переполнение разрядной сетки вычислителя при определении гамма-функций в (2.32) и (2.33).

На рис.3.2 приведены зависимости числа отсчетов N₂ от (в децибелах) при и 10^-6, полученные из (3.7) на основе (2.32) и (2.33). Пунктирными линиями показаны те же зависимости, полученные по приближенным формулам из (2.34) и (2.35). Как видно, погрешность оказывается удовлетворительной.

Время обнаружения узкополосного сигнала равно

. (3.11)

40

Например, пусть и (0 дБ), тогда N₂=160 и в полосе частот f₂=19,5 кГц получим =8,2 мс. С ростом отношения сигнал/шум время обнаружения узкополосного сигнала быстро падает.

Рис. 3.2

3.4. Сравнительный анализ энергетической скрытности

широкополосного и узкополосного сигналов

3.4.1. Анализ энергетической скрытности одиночных

сигналов

Пусть широкополосный и узкополосный сигналы с одинаковой дисперсией (мощностью) занимают полосы частот и соответственно.

Обозначим их отношение через

. (3.12)

41

Это число узкополосных каналов в полосе частот ШПС, причем . Для отношений сигнал/шум можно записать

. (3.13)

Для энергетической скрытности в единицах времени обнаружения широкополосного и узкополосного сигналов получим

, (3.14)

где и - числа отсчетов, необходимые для обнаружения широкополосного и узкополосного сигналов соответственно при заданной достоверности.

Используя аппроксимацию (3.8) (в области h² > 1 появляется погрешность, занижающая значения ), из (3.14) получим

, (3.15)

где d=1,891. Как видно, энергетическая скрытность одиночного широкополосного сигнала значительно выше, чем узкополосного. Например, при , и имеем , N₂=160 и N₁=7.64710⁷, тогда из (3.14)

.

При тех же условиях из приближенного соотношения (3.15) следует

.

42

3.4.2. Анализ энергетической скрытности нескольких

сигналов

Пусть в системе связи действует одновременно сигналов.

Все ШПС действуют в общей полосе частот и их мощности складываются, тогда общее отношение сигнал/шум для сигналов равно

, (3.16)

Узкополосные сигналы располагаются в не перекрывающихся частотных областях, и для каждого из них отношение сигнал/шум определяется (3.13). Для нескольких узкополосных сигналов в общей полосе частот их мощности складываются, но при этом складываются и мощности шума, тогда отношение сигнал/шум равно

(3.17)

и не зависит от числа действующих узкополосных сигналов.

Зависимости и (в децибелах) от числа сигналов при дБ показаны на рис. 3.3. Как видно, с ростом повышается отношение сигнал/шум группы ШПС, которое при становится равным .

Предположим, что разведывательный приемник может расположить все узкополосные сигналы в смежных частотных интервалах с образованием общей полосы частот , где - диапазон частот узкополосного сигнала. ШПС занимает полосу , где M - общее число узкополосных каналов в его полосе. В предыдущих примерах принято = 5 МГц, , =19,5 кГц.

43

Рис. 3.3

С ростом числа ШПС повышается отношение сигнал/шум , за счет этого снижается необходимое для выявления группы ШПС число отсчетов (3.7) при неизменной тактовой частоте и уменьшается время обнаружения , определяющее скрытность группы ШПС.

В рамках принятых допущений увеличение количества узкополосных сигналов не изменяет требуемое число отсчетов, но за счет расширения спектра суммарного сигнала уменьшается интервал между отсчетами, что приводит к падению времени обнаружения , а значит и скрытности группы узкополосных сигналов.

На рис. 3.4 приведены зависимости времени обнаружения (скрытности) группы из ШПС и узкополосных сигналов при исходном отношении сигнал/шум для одного ШПС = -30 дБ, числе узкополосных каналов =256, вероятностях ложной тревоги и пропуска сигнала, равных .

На рис. 3.5 показана зависимость от отношения скрытностей ШПС и узкополосных сигналов

44

. (3.18)

Как видно, при малых k временные затраты на обнаружение достаточно велики и скрытность группы ШПС много выше, чем узкополосных сигналов, различие быстро падает с ростом k.

Рис. 3.4

Рис. 3.5.

45

С учетом аппроксимации (3.8) получим

, (3.19)

и отношение (k) из (3.18) является гиперболической функцией , показанной пунктиром на рис.3.5.

3.5. Применимость параметрических алгоритмов

энергетического обнаружения

Рассмотренные оптимальные алгоритмы энергетического обнаружения случайного сигнала на фоне гауссовского шума требуют знания (измерения) абсолютных значений спектральных плотностей мощности сигнала и помехи .

В простейшем случае решающего правила (2.30) его левая часть представляет собой нормированное к среднеквадратическое значение наблюдаемого процесса [1]

, (3.20)

а правая часть зависит от отношения . При малых из (2.31) приближенно получим

. (3.21)

Для реализации решающего правила (2.30) необходимо обеспечить относительную погрешность определения спектральной плотности мощности шума порядка

46

. (3.22)

Н апример, при получим =10^-3. Если фактическое значение отклоняется от измеренного (относительная погрешность выше ), то достоверность принимаемых решений становится неудовлетворительной. Это поясняет диаграмма на рис. 3.6. Слева показаны значения и , полученные по результатам измерений. По ним выбран порог, с которым сравниваются значения мощности наблюдаемого процесса. Справа Рис. 3.6

показаны фактические

значения и , для которых выбранный порог сильно занижен, что приведет к высокой вероятности ложной тревоги.

Возможность практической реализации оптимального энергетического обнаружителя определяется точностью сведений о спектральных плотностях мощности сигнала и помехи. При высоком отношении сигнал/шум h², характерном для узкополосных сигналов, можно пользоваться приближенными оценками (например, в соседних каналах). Это приведет к потере оптимальности алгоритма обнаружения, однако он останется работоспособным.

При обнаружении ШПС с малым отношением сигнал/шум даже небольшие погрешности в определении, прежде всего, приводят к ухудшению достоверности обнаружения. При высоких погрешностях энергетическое обнаружение ШПС становится практически невозможным.

47