- •§ 1. Задача определения весо-геометрических параметров компоновки. 3
- •Список литературы
- •Введение
- •Задача определения весо-геометрических параметров компоновки.
- •Задача определения баллистических характеристик.
- •§ 1. Задача определения весо-геометрических параметров компоновки.
- •§2. Задача определения аэродинамических характеристик ракеты.
- •§3. Задача определения баллистических характеристик
§3. Задача определения баллистических характеристик
Р
(3.1)
акеты рассматриваемого типа являются одноступенчатыми и имеют однорежимный ракетный двигатель. В этом случае закон изменения скорости по времени включает два участка: стартовый и пассивный. Первый из них характеризуется малой продолжительностью (t =3÷5с) и резким нарастанием скорости полета (ускорение до 250 ÷300 м/с2). Второй участок соответствует свободному полету ракеты по инерции и характеризуется существенным изменением скорости. Рассмотрим методику определения баллистических характеристик ракеты V(t) и S(t)= кʃ0 V(t) dt. [2] Управление движения для стартового участка записано в виде:![]()
З
(3.2)
десь R - тяга двигателя, X - сила лобового сопротивления. Пренебрегая в (З.1) влиянием силы лобового сопротивления и учитывая R = - gJ1, m получим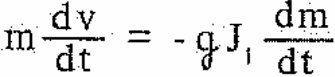
З
(3.3)
десь J1 - удельный импульс топлива. Интегрируя это уравнение с разделяющимися переменными в пределах: по времени - от нуля по tr, но скорости - от начального значения VH до максимального значения Vm получим формулу Цилковского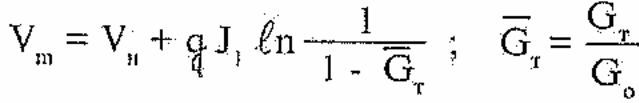
Определим прирост скорости за время стартового участка
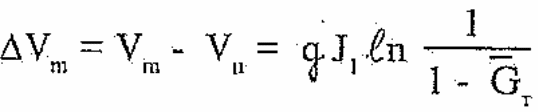
(3.4)
(3.4)
![]()
Зависимость относительного приращения, определенная из (3.4) приведена на рис.3.1,а сплошной линией.
Рассмотрим возможность упрощения формулы (3.4). Полагая
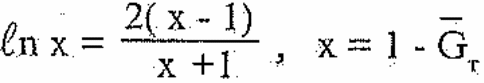
получим
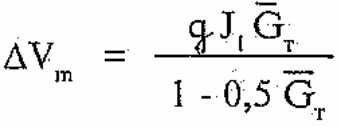
(3.5)
Соответствующая зависимость приведена пунктиром на рис,3.1,а. Физический смысл формулы (3.5) состоит в том, что прирост количества движения под действием импульса тяги определяется по среднему значению веса ракеты на стартовом участке Gn = G0 (1- 0,5 GT). Далее можно получить следующее приближение для формулы (3.4), соответствующее отказу от учета переменности массы.
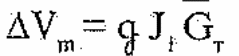
(3.6)
Оценки показывают, что, формулу (З.6) можно применять и при значениях Gт, соответствующих ракетам рассматриваемого типа. Физическое обоснование этого эффекта приведено в [2]. Из (3.6) получим выражение для энерговооруженности ракеты
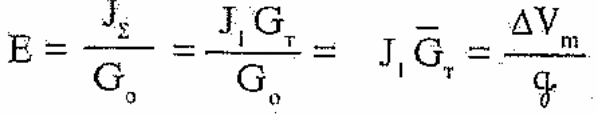
(3.7)
Как следует из (3.7), основным параметром, характеризующим приращение скорости полета на стартовом участке является величина относительного запаса топлива или пропорциональная ему величина энерговооруженности.
Определим допустимый по условиям размещения на ракете запас топлива. Уравнение весового баланса запишем в упрощенном виде (вес конструкции ракеты включаем в полезную нагрузку)
G, = Gmi+(l+α)Gт (3.8)
где α - коэффициент весового совершенства конструкции двигателя.
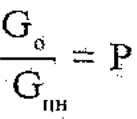
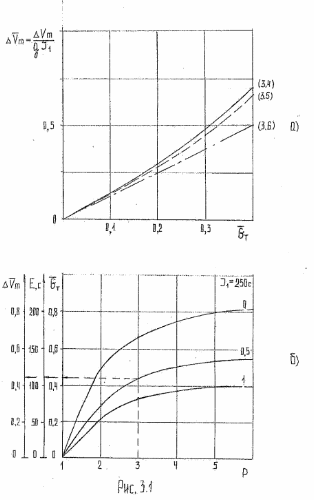
(3.9)
![]()
При проектировании ракеты величины Р и α обычно бывают известны. Тогда из (3.9) может быть определена величина Gт доп. На рис.3.1,б приведена зависимость Gт доп (P) для трех значений величины α.
Поскольку величины Е и ∆Vm пропорциональны величине GT, на вертикальной оси приведены также шкалы для этих величин. Отметим, что дляперспективных ракет рассматриваемого типа Р≈3,0, α=0,5. В этом случае GT= 0,445; Е=110 с. В современных ракетах Е порядка 90 с. Перейдем теперь к рассмотрению пассивного участка полета. Силу лобового сопротивления представим в виде
![]()
где Схо - коэффициент лобового сопротивления при нулевой подъемной силе, ро - плотность воздуха при Н=0, ∆ - относительная плотность. Величина Схо может быть определена по методике проф. Л.С.Чернобровкина. Однако, в целях упрощения мы определим ее косвенно через баллистический коэффициент ракеты ст.

где GK = Go - GT - конечный вес ракеты. В [2] показано, что для ракет рассматриваемого типа величина баллистического коэффициента составляет σ ≈ 2∙10-4 м2/кг. Это значение баллистического коэффициента мы и принимаем для оценочных расчетов.
Перейдем теперь к оценке дальности полета ракеты. Поскольку протяженность стартового участка мала (tr = 3÷5 с), дальность, набираемая ракетой на этом участке, также мала (при мгновенном сгорании топлива Sk = 0) и ее можно не учитывать. В этом случае дальность полета однозначно определяется пассивным участком. Определение этой дальности проведем без учета индуктивного сопротивления Сх инд , полагая Сх = Схо = const. Отметим, что в требованиях ТТЗ обычно задаются дальности пуска на встречных и догонных курсах в режиме стрельбы по неманеврирующей цели, что позволяет принять допущение Сх инд = 0. Из (3.1) при R=0 и Сх = Схо = const получим
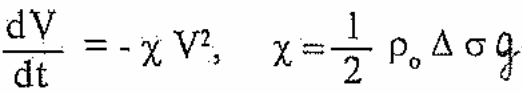
(3.12)
Интегрируя (3.12) от начального значения Vm до текущего значения V, получим
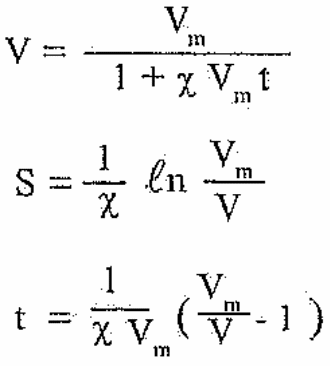
(3.13)
Здесь время отсчитывается от начала пассивного участка, которое можно отождествить с полным временем полета. На основании (3.13) можно получить значение текущих значений скорости V(t) и дальности S(t). На рис.3.2,а приведены зависимости S(V) и t(V) , где V = V/Vm, на рис.3.2,6 зависимости V(t) и S(t). Для определения полной дальности полета необходимо задать значение конечной скорости полета - VK, которая зависит от ракурса стрельбы.
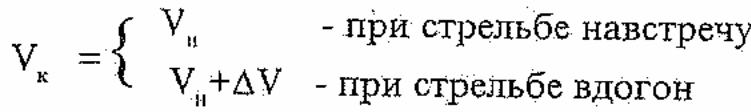
(3.14)
где ∆V - запас скорости. Обычно ∆V=150 м/с. Подставляя (3.14) в (3.13) определим полные дальности пуска ракеты. Заданные в ТТЗ дальности пуска определяются выражениями
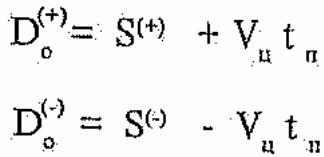
(3.15)
где S(+) - соответствует конечной скорости Vк = Vн , S(-) - соответствует конечной скорости Vк = Vн + 150.
Используя полученные соотношения, проведем оценку баллистических характеристик рассматриваемой ракеты. Положим Go=170 кг; Gт = 60 кг; Ji =240 с; ϭ = 1,7-10-4 m2/ кг; Нн=Нц=10 км; Vн=Vц-600 м/с.
Относительный запас топлива
![]()
Энерговооруженность
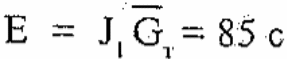
Приращение скорости на стартовом участке
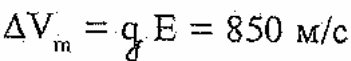
Скорость в конце стартового участка
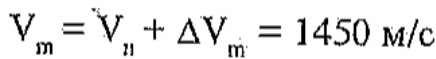
Коэффициент χ. При ро = 0,125; ∆= 0,34; ϭ=1,7∙10-4 получим
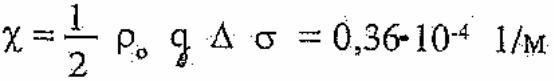
Дальность полета на встречных курсах
![]()
Дальность полета на догонных курсах
![]()
Время полета на встречных курсах
![]()
Время полета на догонных курсах

Дальность пуска на встречных курсах
![]()
Дальность пуска догонных курсах
![]()
Аналогичным образом определяются баллистические характеристики для других режимов пуска, определяемых величинами Ннц и Vнц.