
- •1 Вопрос Модель распространения радиоволн в условиях прямой видимости.
- •2 Вопрос Амплитудная модуляция гармонического сигнала. Угловая модуляция гармонического сигнала.
- •3 Вопрос Биполярные транзисторы: Структура транзистора. Режимы работы. Схема включения. Характеристики и параметры (11 б 3 в) 7б 3 вопрос
- •Основная область применения любых транзисторов — усиление слабого сигнала за счет дополнительного источника питания.
- •Устройство биполярного транзистора
- •Работа биполярного транзистора.
- •Режимы работы биполярного транзистора
- •Основные параметры биполярного транзистора.
БИЛЕТ 25
1 Вопрос Модель распространения радиоволн в условиях прямой видимости.
Расстояние между передающей и приемной антеннами, прикотором прямая линия, соединяющая эти антенны, касается поверхности Земли
Как правило под радиорелейной связью понимают именно радиорелейную связь прямой видимости.
При построении радиорелейных линий связи антенны соседних радиорелейных станций располагаются в пределах прямой видимости. Требование наличия прямой видимости обусловлено возникновением дифракционных замираний при полном или частичном закрытии трассы распространения радиоволн. Потери при дифракционных замираниях могут вызывать сильное ослабление сигнала, таким образом радиосвязь между соседними радиорелейными станциями станет невозможна. Поэтому для устойчивой радиосвязи антенны соседних радиорелейных станций как правило располагают на естественных возвышенностях или специальных телекоммуникационных башнях или мачтах таким образом, чтобы трасса распространения радиоволн не имела препятствий.
С учетом ограничения на необходимость наличия прямой видимости между соседними станциями дальность радиорелейной связи ограничена как правило 40 - 50 км.










2 Вопрос Амплитудная модуляция гармонического сигнала. Угловая модуляция гармонического сигнала.
Амплитудная модуляция – процесс изменения амплитуды несущего колебания, соответствующего изменению непрерывного информационного сигнала [21, 32, 39].
При амплитудной модуляции мгновенная амплитуда несущего колебания:
|
(2.2) |
где ![]() –
амплитуда несущей;
–
амплитуда несущей; ![]() –
коэффициент пропорциональности,
выбираемый так, чтобы амплитуда
–
коэффициент пропорциональности,
выбираемый так, чтобы амплитуда ![]() всегда
была положительной. Частота и фаза
несущего гармонического колебания при
AM остаются неизменными.
всегда
была положительной. Частота и фаза
несущего гармонического колебания при
AM остаются неизменными.
Для
математического описания AM сигнала в
(2.2) вместо коэффициента ![]() ,
зависящего от конкретной схемы модулятора,
вводится индекс модуляции:
,
зависящего от конкретной схемы модулятора,
вводится индекс модуляции:
|
(2.3) |
т.е.
отношение разности между максимальным
и минимальным значениями амплитуд AM
сигнала к сумме этих значений. Для
симметричного модулирующего сигнала ![]() AM
сигнал также симметричный, т.е.
AM
сигнал также симметричный, т.е. ![]() .
Тогда индекс модуляции равен отношению
максимального приращения амплитуды, к
амплитуде несущей.
.
Тогда индекс модуляции равен отношению
максимального приращения амплитуды, к
амплитуде несущей.
|
(2.4) |
Физически
индекс модуляции характеризует собой
глубину амплитудной модуляции и может
изменяться в пределах ![]() .
.
Таким образом для любого AM сигнала справедливо:
|
(2.5) |
Амплитудная
модуляция гармоническим колебанием.
В простейшем случае модулирующий сигнал
является гармоническим колебанием с
частотой ![]() .
При этом выражение
.
При этом выражение
|
(2.6) |
соответствует однотональному AM сигналу, представленному на рис. 2.26.

Однотональный
AM сигнал можно представить в виде суммы
трех гармонических составляющих с
частотами: ![]() –
несущей;
–
несущей; ![]() –
верхней боковой и
–
верхней боковой и ![]() –
нижней боковой:
–
нижней боковой:
|
(2.7) |
Спектральная
диаграмма однотонального AM сигнала,
построенная по (2.7), симметрична
относительно несущей частоты
(рис.
2.2,в). Амплитуды боковых колебаний с
частотами
и
одинаковы
и даже при ![]() не
превышают половины амплитуды несущего
колебания
.
не
превышают половины амплитуды несущего
колебания
.
Гармонические
модулирующие сигналы и соответственно
однотональный AM сигнал на практике
встречаются редко. В большинстве случаев
модулирующие первичные
сигналы
являются сложными функциями времени
(рис.2.3,а). Любой сложный сигнал
можно
представить в виде конечной или
бесконечной суммы гармонических
составляющих, воспользовавшись рядом
или интегралом Фурье.
Каждая гармоническая составляющая
сигнала
с
частотой ![]() приведет
к появлению в AM сигнале двух боковых
составляющих с частотами
приведет
к появлению в AM сигнале двух боковых
составляющих с частотами ![]() .
.
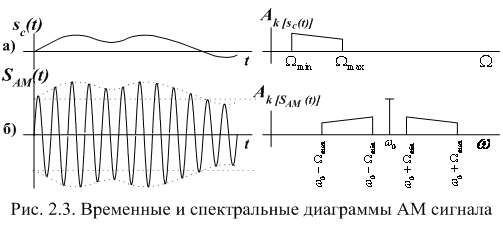
Множеству
гармонических составляющих в модулирующем
сигнале с частотами ![]() будет
соответствовать множество боковых
составляющих с частотами
будет
соответствовать множество боковых
составляющих с частотами ![]() .
Для наглядности такое преобразование
спектра при AM показано на рис. 2.3,б. Спектр
сложномодулированного AM сигнала, помимо
несущего колебания с частотой
,
содержит группы верхних и нижних боковых
колебаний, образующих соответственно
верхнюю боковую полосу и нижнюю боковую
полосу AM сигнала.
.
Для наглядности такое преобразование
спектра при AM показано на рис. 2.3,б. Спектр
сложномодулированного AM сигнала, помимо
несущего колебания с частотой
,
содержит группы верхних и нижних боковых
колебаний, образующих соответственно
верхнюю боковую полосу и нижнюю боковую
полосу AM сигнала.
При этом верхняя боковая полоса частот является масштабной копией спектра информационного сигнала, сдвинутого в область высоких частот на величину . Нижняя боковая полоса частот также повторяет спектральную диаграмму сигнала , но частоты в ней располагаются в зеркальном порядке относительно несущей частоты .
Ширина
спектра AM сигнала ![]() равна
удвоенному значению наиболее высокой
частоты
равна
удвоенному значению наиболее высокой
частоты ![]() спектра
модулирующего низкочастотного сигнала,
т. е.
спектра
модулирующего низкочастотного сигнала,
т. е. ![]() .
.
Наличие
двух боковых полос обусловливает
расширение занимаемой полосы частот
примерно в два раза, по сравнению со
спектром информационного сигнала.
Мощность, приходящаяся на колебание
несущей частоты, постоянна. Мощность,
заключенная в боковых полосах, зависит
от индекса модуляции и увеличивается
с увеличением глубины модуляции. Однако
даже в крайнем случае, когда ![]() ,
только
,
только ![]() всей
мощности колебания приходится на две
боковые полосы.
всей
мощности колебания приходится на две
боковые полосы.
Угловая модуляция - это общее название двух тесно связанных между собой видов модуляции - частотной (ЧМ) и фазовой (ФМ). В системах с частотной модуляцией информация передается изменением мгновенной частоты несущего колебания, а при фазовой модуляции модулирующий сигнал изменяет непосредственно фазу несущего колебания. Угловая модуляция обычно применяется, когда требуется обеспечить высокую достоверность приема передаваемого сообщения. Это объясняется тем, что системы с угловой модуляцией обладают повышенной по сравнению с AM помехоустойчивостью. Рассмотрим немодулированное несущее колебание
где
И
полезный сигнал (передаваемое
сообщение) При угловой модуляции
где функция θ(t) несет передаваемое сообщение. При j0 = 0 модулированное колебание
Для изучения свойств угловой модуляции полезно использовать понятие мгновенной частоты f(t), которая определяется по формулам:
то есть мгновенная угловая частота - это скорость изменения полной фазы. При θ(t) = 0, w(t) = w. При фазовой модуляции (ФМ) модулирующий сигнал непосредственно изменяет фазу несущей, то есть изменения фазы равно
где kj – коэффициент пропорциональности, который называется индексом фазовой модуляции. Соответственно, уравнение ФМ – сигнала определяется выражением:
В частном случае гармонического модулирующего колебания
Пример однотонального ФМ – сигнала приведен на рис. 2.18.
С
увеличением значений
При
частотной модуляции (ЧМ) отклонения
мгновенной частоты относительно
kf – коэффициент частотной модуляции, имеющий размерность Гц/В. Соответственно, полная фаза колебаний:
Выражение для ЧМ колебания имеет вид
Введем характеристики угловой модуляции: индекс модуляции и девиацию частоты. Индексом модуляции называется максимальное отклонение фазы несущего колебания
Для ФМ сигнала
При частотной модуляции отклонение мгновенной частоты от несущей равно
h(t) £ 1 – нормированное отклонение частоты,
Рассмотрим частный случай гармонического модулирующего колебания. . В этом случае
Модулированный сигнал
где Итак, в случае гармонического модулирующего колебания индекс частотной модуляции равен отношению максимальной девиации частоты к частоте модулирующего колебания. Спектр при угловой модуляции значительно сложнее спектра при AM. Полоса спектра сигнала с УМ
При |

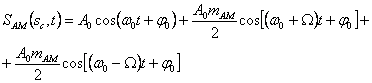 .
. ,
, Рис.
2.18. Фазомодулированный сигнал
Рис.
2.18. Фазомодулированный сигнал ,
или
,
или  .
. .
.