Консервативті жүйенің еркін тербелісінің дифференциалдық теңдеуі және оның жалпы шешімі

Еркіндік дәрежесі шекті сан болатын консервативті жүйенің еркін тербелісінің дифференциалдық теңдеуін Лагранждың келесі теңдеуінен алуға болады:

Мұндаңы s – қарастырып отырған жүйенің еркіндік дәреже саны.

Жалпыланған координаттың бас нүктесі ретінде жүйенің тепе-теңдік күйін алайық, яғни бұл орында - жалпыланған координаталар нөлге тең деп аламыз.

Жүйенің кинетикалық энергиясы:

Жүйенің потенциалдық энергиясы:

ал

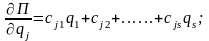
болса, онда Лагранж теңдеуі тұрақты коэффициентті екінші ретті сызықты біртекті дифференциалдық теңдеулер жүйесіне келтіріледі:

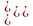(4.1.1)

(4.1.1) теңдеуі s еркіндік дәрежелі жүйенің еркін тербелісін анықтайды.

шамаларын инерция коэффициенттері деп, ал шамаларын қатаңдық коэффициенттері деп атаймыз.

Бұл теңдеулердің дербес шешімдері мына түрде болады:

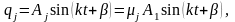
мұндағы

мәндерін (4.1.1) теңдеуіне қою арқылы алатынымыз:

(4.1.2)

Егер бұл жүйенің анықтаушы нөлге тең болса, онда (4.1.2) сызықты және біртекті алгебралық теңдеулер жүйесінің белгісіз тұрақтылары -ге қарағанда нөлден өзге шешімі болады, бұл шарттан еркін тербелісті жүйенің жиілігінің келесі тіңдеуін аламыз:

(4.1.3)

(4.1.3) теңдеуі -қа қарағандағы s-ші дәрежелі теңдеу болып табылады; бұл теңдеуден еркін тербелісті жүйенің барлық жиіліктерін анықтауға болады, себебі -жиіліктер теңдеуінің түбірі- заттық және оң шамалар (жүйенің орнықты тепе-теңдік орнының маңындағы кіші тербелісі қарастырылады).

-ң барлық табылған мәндерін (4.1.2) теңдеуіне қойсақ 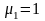және де бұл теңдеулердің қандай да бір біреуі (мысалы, бірінші) қалғанынан анықталады десек, (себебі анықтауыш 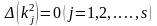онда барлық коэффициенттерін анықтау үшін мынадай алгебралық теңдеулер жүйесін аламыз:

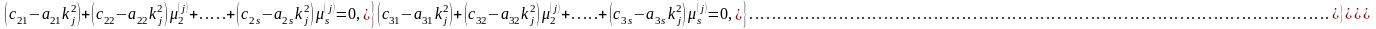(4.1.4)

Бұл теңдеулерден

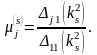….. (4.1.5)

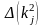Мұндағы - негізгі анықтауышынан бірінші жол мен бірінші бағанды өшіру нәтижесінде алынған анықтауыш; - осы негізгі анықтауыштың таңбасы деп алынған бірінші жол мен j- бағанның элементінің миноры; -бірге тең таралу коэффициенттері.

Сонымен, жүйенің еркін тербелісінің (4.1.1) дифференциалдық теңдеулерінің дербес шешімдері келесі түрде болады:

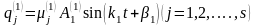теңдеулері жиілікті және бастапқы фазалы жүйенің бірінші бас тербелісін анықтайды;

жиілігі және бастапқы фазасы 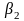болатын екінші бас тербелісті анықтайды және т.с.с.

коэффициенттері сәйкесінше бірінші бас тербелістің формасын, екінші бас тербелістің 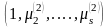формасын және т.с.с. анықтайды.

және тұрақты шамалары анықталмаған болып табылады.

(4.1.1) теңдеулері сызықты болғандықтан, бұл теңдеулердің жалпы шешімін сәйкес дербес шешімдердің қосындысы ретінде табуға болады.

Бұл теңдеуді ашып жазатын болсақ,

....................................................................................................... (4.1.6)

және белгісіз тұрақтылардан2s шамаларын және бастапқы шарттардан анықталады, яғни бастапқы жалпыланған жылдамдықтармен бастапқы жалпыланған координаталар арқылы келесі теңдеулерден:

(4.1.7)

Сонымен, s еркіндік дәрежелі еркін тербелісті жүйені толық зерттеу үшін:

1. (4.1.3) теңдеуден бос тербелістің жиіліктерін табу қажет;

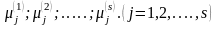2. (4.1.5) формулаларынан таралу коэффициенттерін есептеу қажет;

3. (4.1.7) теңдеулерінен амплитудалары мен бастапқы фазаларын табу қажет.

Егер еркіндік дәреже саны s>4 болса, онда бұл есепті толық шешу үшін өте үлкен есептеу жұмысын жасау қажет.

Техникалық қосымшаларда аса маңызды мәнде, әдетте, тек бірінші (негізгі) жиілік пен жүйенің еркін тербелісінің бірінші (негізгі) формасы алынатын болғандықтан, көп жағдайда есепті шешу бірінші бас тербелістің тек жиілігі мен формасын анықтаумен шектелуі мүмкін.

Жүйенің бірінші бас тербелісінің жиілігі мен формасын анықтау үшін әр түрлі жуықталған әдістер қолданылады, себебі еркіндік дәрежесі үлкен сан болатын жүйе жағдайында есептің нақты шешімін алу мүмкін емес.