
- •Динамикалық коэффициент
- •Лездік күш импульсін тудыратын бірлік еркіндік дәрежелі жүйенің мәжбүр тербелісі
- •Сызықсыз кедергі жағдайындағы мәжбүр тербеліс. Тұтқырлықтың эквиваленттік коэффициенті.
- •Консервативті жүйенің еркін тербелісінің дифференциалдық теңдеуі және оның жалпы шешімі
- •Инерция, қатаңдық коэффициенттері мен әсер ету коэфициенттерінің матрицалары
- •Нүктенің еркін тербелісінің негізгі жиілігін жуықтап анықтау әдісі
- •Топсалы ферманың еркін тербелісінің жиілігін анықтау
- •Жүйенің еркін тербелісінің бас координатамен алынған дифференциалдық теңдеуінің жалпы шешімі
Резонанс және соққы құбылысы
Егер мәжбүр тербелістің қандай да бір жиілігі – ұйытқушы күштің қандай да бір гармоникасының жиілігі жүйенің еркін тербелісінің жиілігіне тең болса, яғни
jp=
k, (j=1,2,…, )
)
онда j- реттік резонанс пайда болады.
jp= k жиілігі дағдарысты (қауіпті) жиілік деп аталады. Бұл жағдайда (5.3.8) формуласы бойынша амплитуда мынаған тең:
 =
=
 (5.4.1)
(5.4.1)
Бұл
жағдай үшін (5.3.9) формула бойынша
 ,онда фазалық ығысуы:
,онда фазалық ығысуы:
 және
және
 .
.
Өшу
коэффициенті
 -
нің аз мәнінде
амплитудасы (5.3.6) қатардың басқа
гармоникаларының амплитудасымен
салыстырғанда өте үлкен болуы мүмкін,
әсіресе егер бірінші ретті резонанс
туатын болса, өйткені ұйытқушы күштің
бірінші гармоникалық амплитудасы:
-
нің аз мәнінде
амплитудасы (5.3.6) қатардың басқа
гармоникаларының амплитудасымен
салыстырғанда өте үлкен болуы мүмкін,
әсіресе егер бірінші ретті резонанс
туатын болса, өйткені ұйытқушы күштің
бірінші гармоникалық амплитудасы:
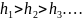
Бұл жағдай үшін (5.3.4) теңдеуін қарапайым теңдеумен алмастыруға болады:
(5.4.2)
(5.4.2) теңдеуі жеткілікті дәлдікпен бірінші ретті резонанстық теңдеуі анықтайды.
Мәжбүр
тербелістің
амплитудасы,
 ығысу фазасы салдарынан максимум мәніне
ығысу фазасы салдарынан максимум мәніне
 jp=
k резонанста
емес,
jp=
k резонанста
емес,
 - дің басқа мәнінде жететінін ескерту
қажет.
- дің басқа мәнінде жететінін ескерту
қажет.
Амплитуданың
максимумына түбір астындағы өрнектің
минимумы сәйкес келеді.
Осы өрнекте бойынша туынды алып және оны нөлге теңестіріп мына теңдікті аламыз:
Егер
болса,

болғанда, максимумы болмайды және бұл жағдайда резонанс жоқ.
анықтайтын
формулаға
 мәнін қойып мынаны аламыз:
мәнін қойып мынаны аламыз:
(5.4.3)
Өшу коэффициентінің аз мәнінде
яғни амплитудасының максимал мәні және оның резонанстағы мәні бір-біріне өте жақын (бірдей) деп алуға болады.
Резонанстан жеткілікті алыс аймақта, орныққан тәртіпте және өшу коэффициенті аз болғанда кедергі күшін ескермеуге болады.
Бұл жағдай үшін жүйенің мәжбүр тербелісінің теңдеуі мына түрде болады:
(5.4.4)
мұндағы
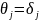 және
және
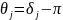 .
.
Егер
 0
және резонанс туатын болса (jp=
k),
онда
0
және резонанс туатын болса (jp=
k),
онда
яғни (5.4.4) теңдеуі жүйенің мәжбүр тербелісін анықтамайды.
Осы жағдайды зерттеу үшін ұйытқушы күштің қандай да бір гармоникасы тудыратын мәжбүр тербелісті қарастырайық. Мысалға бірінші гармониканы алайық және еркін тербелісті ескерейік.
0 болғандықтан, (5.3.10) теңдеуі мынандай түрде болады.
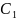 және
және
 тұрақтыларды
тұрақтыларды
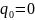 ;
;
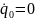 бастапқы шарттар арқылы табамыз:
бастапқы шарттар арқылы табамыз:
Сонымен,
(5.4.5)
; бастапқы шарты нәтижесінде пайда болатын еркін тербелісті тудыратын ұйытқушы күш болады.
Егер
p=k,
онда
(5.4.5) теңдеудің оң жағы анықталмаушылықтың
 түріне айналады.
түріне айналады.
Осы анықталмаушылықты ашу арқылы мынаны аламыз:
(5.4.6)
Резонанс жағдайында (5.4.6) теңдеуінің екінші мүшесіне сәйкес келетін мәжбүр тербелістің амплитудасы уақыттың өзгеруімен қатар тура пропорционалдық заңы бойынша шексіз артады:
Уақыт өтуімен амплитудасы үздіксіз артатын резонанстық тербелістің графигі 26-суретте көрсетілген.
Резонанстан бөлек, кедергіні ескермей соққы құбылысын қарастырайық. Соққы құбылысы мәжбүр тербелістің p жиілігі, еркін тербелістің жиілігі k – дан айырмашылығы аз болған жағдайда туады.
Дербес жағдай үшін:
Тербеліс резонансқа жақын аймақта жүреді.
26-сурет
(5.4.5) теңдеуінен
немесе
(5.4.7)
(5.4.7) теңдеуі жүйенің соққы жағдайындағы мәжбүр тербелісін анықтайды.
Бұл тербелістің амплитудасы
уақыттың баяу өзгеретін периодты функциясы болады.
Оның периоды:
Мәжбүр
тербелістің периоды:
 .
.
 болғандықтан
болғандықтан
 .
.
Мәжбүр тербеліс графигі 27-суретте көрсетілген.
Қарастырылған соққы тербелісі өшу коэффициенті 0 болғанда туындайды, яғни кедергі күші ескерілмейді.
Ұйытқушы
күштің негізгі жиілігі
 жуықтап алғанда өшетін тербеліс жиілігі
жуықтап алғанда өшетін тербеліс жиілігі
 - қа тең болған жағдайда, кедергі күшінің
тербеліске ықпалын зерттейік.
- қа тең болған жағдайда, кедергі күшінің
тербеліске ықпалын зерттейік.
Өшетін
тербелісті ескеріп және
 деп ұйғарып мынаны аламыз:
деп ұйғарып мынаны аламыз:
27-сурет
мұндағы
және тұрақтыларды ; бастапқы шарты үшін мынадай мәнге ие болады
Сондықтан
Бұл теңдеуді мынадай түрде бейнелейік
немесе
28-сурет. Өшетін соққы тербелісінің графигі
(5.4.8) теңдеудің бірінші мүшесі жүйенің өшпейтін мәжбүр тербелісін анықтайды және амплитуда
ал периоды
А(t) амплитудасының өзгеру периоды
Сонымен,
нақты жағдайда ( 0)
ұйытқушы күш тудыратын, жиілігі өшетін
тербеліс жиілігіне жақын келетін соққы
тербелісі жүйенің бастапқы қозғалыс
кезеңінде және өшу коэффициенті
аз болған жағдайда болады (28-сурет).
0)
ұйытқушы күш тудыратын, жиілігі өшетін
тербеліс жиілігіне жақын келетін соққы
тербелісі жүйенің бастапқы қозғалыс
кезеңінде және өшу коэффициенті
аз болған жағдайда болады (28-сурет).
Орныққан тәртіпте қозғалыс иеңдеуі мына теңдеу арқылы анықталады.
Нақты
жағдайда өшетін соққы тербелісі
жиіліктері
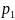 және
және
 бір-біріне өте жақын болатын екі ұйытқушы
күштердің әсерінен болады.
бір-біріне өте жақын болатын екі ұйытқушы
күштердің әсерінен болады.
Бұл жағдай ұшін жүйенің мәжбүр тербелісінің теңдеуі мына түрде болады:
(5.4.9)
Мұнда
 тербелістің бастапқы ығысу фазасы.
тербелістің бастапқы ығысу фазасы.
Белгілеу енгізейік
(5.4.9) теңдеуі мынадай түрді қабылдайды:
Бұдан кейін
деп аламыз, онда
немесе
(5.4.10)
мұндағы
(5.4.10)
теңдеуі өшпейтін соққы тербелісін
анықтайды. Бұл тербелістің
А(t)
амплитудасы уақыттың өтуімен
................... дейін баяу өзгередім( -
аз шама)
-
аз шама)
дербес жағдай үшін
(5.4.11)
Динамикалық коэффициент
Периодты ұйытқушы күш тудыратын мәжбүр тербелістің амплитудасын анықтайтын (5.3.8) формуланы мынадай түрде бейнелейік:

 (5.5.1)
(5.5.1)
Мұндағы

 күшінің статикалық әсерінде, яғни егер
күшінің статикалық әсерінде, яғни егер
 болғанда, жүйенің тепе-теңдік орнынан
ауытқуы мынаған тең:
болғанда, жүйенің тепе-теңдік орнынан
ауытқуы мынаған тең:

себебі
 .
.
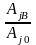 қатынасы
динамикалық
коэффициент деп
аталады:
қатынасы
динамикалық
коэффициент деп
аталады:
 (5.5.2)
(5.5.2)
Ұйытқушы
күштің
 -
гармоникасына сәйкес келетін динамикалық
коэффициент
-
гармоникасына сәйкес келетін динамикалық
коэффициент
 (5.5.3)
(5.5.3)
n
және k берілген қатынасында динамикалық
коэффициент
 –дің функциясы болады:
–дің функциясы болады:

Егер
өшу коэффициенті
 болса, (кедергі ескерілмейді) онда
болса, (кедергі ескерілмейді) онда
 (5.5.4)
(5.5.4)
- реттік резонанс жағдайында (5.4.1) формула бойынша

Бұл жағдай үшін
 (5.5.5)
(5.5.5)
Бұны (5.5.3) формулада тікелей алуға болады, өйткені 5-ші реттік резонанс үшін

Мәжбүр тербеліс амплитудасының максимал мәні (5.4.3) формуласымен анықталады:
 (5.5.6)
(5.5.6)
динамикалық коэффициенттің максимал мәні
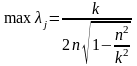 (5.5.7)
(5.5.7)
29-сурет 30-сурет
Өшу коэффициенті n аз мәнінде (5.5.5) және (5.5.7) формулалары бойынша бірдей нәтиже алуға болады, яғни максималды динамикалық коэффициент және резонанстағы динамикалық коэффициент бір-біріне өте жақын болады.
29-30
суреттерде
 функциясының
функциясының
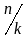 қатынасының әр түрлі мәні үшін графигі
көрсетілген, яғни динамикалық
коэффициенттің өзгеру графигі.
қатынасының әр түрлі мәні үшін графигі
көрсетілген, яғни динамикалық
коэффициенттің өзгеру графигі.
 мәні
0-ден
мәні
0-ден
 дейін өзгергенде,
дейін өзгергенде,
 динамикалық
коэффициенттің мәні 1-ден 0-ге дейін
өзгереді.
динамикалық
коэффициенттің мәні 1-ден 0-ге дейін
өзгереді.
Лездік күш импульсін тудыратын бірлік еркіндік дәрежелі жүйенің мәжбүр тербелісі
 Өте
аз
Өте
аз
 уақыт интервалында, импульсі шектелген
күшті лездік
күш деп
атайды. Лездік күш импульсі мына түрде
жазылады:
уақыт интервалында, импульсі шектелген
күшті лездік
күш деп
атайды. Лездік күш импульсі мына түрде
жазылады:
Бұндай
импульстер, мысалы, денелердің соқтығысуы
кезінде пайда болады. Осындай импульстерден
пайда болатын тербелістерді зерттеу
үшін
 және
және
 бастапқы шарттарды қанағаттандыратын
мәжбүр тербелістің дифференциалдық
тедеуінің жалпы шешімін пайдаланамыз.
Бұл жағдай үшін теңдеу мына түрде
жазылады (5.2.5):
бастапқы шарттарды қанағаттандыратын
мәжбүр тербелістің дифференциалдық
тедеуінің жалпы шешімін пайдаланамыз.
Бұл жағдай үшін теңдеу мына түрде
жазылады (5.2.5):
 .
.
Алдымен,
тұрақты жалпыланған күштің
 уақыт мезетінде кенеттен қосылып, және
уақыт интервалы бойы әсер етуінен
туатын тербеліс теңдеуін табайық.
(5.2.5) формуласын қолданып мынаны аламыз.
уақыт мезетінде кенеттен қосылып, және
уақыт интервалы бойы әсер етуінен
туатын тербеліс теңдеуін табайық.
(5.2.5) формуласын қолданып мынаны аламыз.


немесе
 (5.6.1)
(5.6.1)
(5.6.1)
теңдеуімен анықталатын тербеліс
 күшінің
әсері тоқтағанға дейін болады, яғни
егер
күшінің
әсері тоқтағанға дейін болады, яғни
егер
 .
.
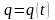 координатаның
максимал мәнін анықтайық.
координатаның
максимал мәнін анықтайық.
(5.6.1) теңдеуінен мынаны аламыз:
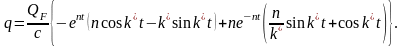
Жалпыланған
 жылдамдықты нөлге теңестіріп мынаны
аламыз:
жылдамдықты нөлге теңестіріп мынаны
аламыз:

t шектік мәні мынадай шартқа әкеледі:

Себебі t=0 болғанда, .
Сондықтан
q максимал мәніне
 болғанда,
яғни t уақыт аралығы өтетін тербелістің
жарты периодына тең болған дағдайда
жетеді.
болғанда,
яғни t уақыт аралығы өтетін тербелістің
жарты периодына тең болған дағдайда
жетеді.
Максимал мән
 (5.6.2)
(5.6.2)
Күштің статикалық әсерінен

Онда
қарастырылған жағдай үшін
 динамикалық коэффициент
динамикалық коэффициент
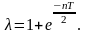 (5.6.3)
(5.6.3)
Бұл коэффициент барлық кезде 1-ден үлкен.
n=0 жағдай үшін (кедергі ескерілмейді) (5.6.1) теңдеуі мынадай түрде болады
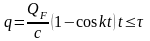 (5.6.4)
(5.6.4)
Кенеттен
түсірілген тұрақты күштің динамикалық
әсері бұл жағдайда (5.6.3) формула бойынша
статикалықтан 2 есе үлкен,
 болады.
болады.
Күштің
әсері тоқтағаннан кейін
 жүйе тербелісінің теңдеуін келесі түрде
алуға болады:
жүйе тербелісінің теңдеуін келесі түрде
алуға болады:
 уақыт мезетінде, жүйеге түсірілген
-
жалпыланған күші (5.6.1) теңдеуіне ұқсас
теңдеумен анықталатын тербеліс тудырады,
атап көрсеткенде
уақыт мезетінде, жүйеге түсірілген
-
жалпыланған күші (5.6.1) теңдеуіне ұқсас
теңдеумен анықталатын тербеліс тудырады,
атап көрсеткенде

Осы
тербеліске
 уақыт мезетінде жүйеге түсірілген
уақыт мезетінде жүйеге түсірілген
 күштің әсерінен туатын тербелісті
қосып,
жағдайы үшін тербеліс теңдеуін аламыз.
күштің әсерінен туатын тербелісті
қосып,
жағдайы үшін тербеліс теңдеуін аламыз.
Мұндағы
 күші әсерінің ұзақтығы
болғанда
күші әсерінің ұзақтығы
болғанда
 (5.6.5)
(5.6.5)
Егер
 , онда теңдеуімен анықталатын жалпыланған
координата, өзінің максимал мәніне
күштің әсері тоқтағаннан кейін жетеді,
яғни қандай да бір
, онда теңдеуімен анықталатын жалпыланған
координата, өзінің максимал мәніне
күштің әсері тоқтағаннан кейін жетеді,
яғни қандай да бір
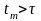 уақыт моментінде. Осы уақыт моментін
төмендегі теңдеуден анықтауға болады:
уақыт моментінде. Осы уақыт моментін
төмендегі теңдеуден анықтауға болады:
 (5.6.6)
(5.6.6)
(5.6.6) қатынасы q-дің мынадай максимал мәнін алуға мүмкіндік береді
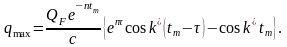 (5.6.7)
(5.6.7)
Бұдан динамикалық коэффициент:
 (5.6.8)
(5.6.8)
Егер n шамасы k шамасынан анағұрлым кіші болса, онда кедергіні ескермеуге болады. Бұл жағдайда барлық формула (n=0) ықшамдалады және мынадай түрге ие болады:
 (5.6.9)
(5.6.9)
 (5.6.10)
(5.6.10)
 (5.6.11)
(5.6.11)
 (5.6.12)
(5.6.12)
Жүйеге
кенеттен түсірілген тұрақты
күшінің әсер ету ұзақтығына тәуелді
болуына байланысты (5.6.8) және (5.6.12)
формулаларымен анықталатын
 коэффициенті
бірден үлкен және кіші болуы мүмкін.
коэффициенті
бірден үлкен және кіші болуы мүмкін.
 лездік
импульсті тудыратын тербелісті зерттеу
үшін (5.6.5) теңдеуін мына түрде бейнелейік.
лездік
импульсті тудыратын тербелісті зерттеу
үшін (5.6.5) теңдеуін мына түрде бейнелейік.
 .
.
Осы
өрнектің оң жағы
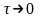 болғанда
болғанда
 анықталмаушылыққа әкеледі. Осы
анықталмаушылықты Лопиталь әдісімен
ашып, мынаны аламыз
анықталмаушылыққа әкеледі. Осы
анықталмаушылықты Лопиталь әдісімен
ашып, мынаны аламыз

немесе
 (5.6.13)
(5.6.13)
Бұдан q-ң максимал мәні
 (5.6.14)
(5.6.14)
мұндағы
 (5.6.15)
(5.6.15)
Өшу
коэффициенті n-ң аз мәні үшін
 болғанда
болғанда

 (5.6.16)
(5.6.16)
Егер n=0, онда
 (5.6.17)
(5.6.17)
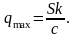 (5.6.18)
(5.6.18)
 шамасын,
статикалық әсері S лездің импульстің
әсерінен тепе-теңдік орнынан максимал
ауытқуын көрсететін эквивалентті
жалпыланған күш деп қарауға болады.
шамасын,
статикалық әсері S лездің импульстің
әсерінен тепе-теңдік орнынан максимал
ауытқуын көрсететін эквивалентті
жалпыланған күш деп қарауға болады.
Лездік импульстер жүйесінің әсерінен туатын тербелісті қарастырайық.
Егер импульс

уақыт
аралықтарында пайда болса, мұндағы
s-импульс
саны, онда
 болғанда
мәжбүр тербелістің теңдеуі мына түрде
болады:
болғанда
мәжбүр тербелістің теңдеуі мына түрде
болады:
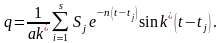 (5.6.19)
(5.6.19)
Тең
импульстер
 және тең уақыт аралықтары үшін
және тең уақыт аралықтары үшін
 :
:
 (5.6.20)
(5.6.20)
Егер пайда болған импульстер арасындағы уақыт аралығы
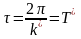
болса, онда соққылы резонанс болады.
Бұл жағдайда
 (5.6.21)
(5.6.21)
Уақыттың
санақ басы ретінде
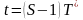 моментін қабылдап, мынаны аламыз.
моментін қабылдап, мынаны аламыз.
 (5.6.22)
(5.6.22)
немесе
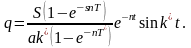
Егер n=0 онда (5.6.22) бойынша
 (5.6.23)
(5.6.23)
мұнда s-импульс саны.
31-сурет.
Шексіз
рет периодты түрде пайда болатын лездік
күштің импульсі үшін
 ,
(5.6.22) теңдеу мынадай түрде болады:
,
(5.6.22) теңдеу мынадай түрде болады:
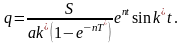 (5.6.24)
(5.6.24)
Бұл
теңдеуді
 интервалы үшін қолдануға болады.
интервалы үшін қолдануға болады.
Келесі интервалдар үшін цикл қайталанады, яғни жүйенің қозғалысы осы теңдеумен анықталады. Оның графигі 31-суретте көрсетілген.
Кедергі
болмаған жағдайда (n=0) тербеліс амплитудасы
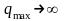 ,
яғни импульс саны артуымен (5.6.24) формула
бойынша амплитуда шексіз артады.
,
яғни импульс саны артуымен (5.6.24) формула
бойынша амплитуда шексіз артады.
Бұл тербелістің өсу графигі 32-суретте көрсетілген.
32-сурет.
Сонымен, соққылы резонанс бар кезінде периодты ауытқушы күшінің әсер ету нәтижесінде пайда болған резонанстар жағдайындағы сияқты аз өшу коэффициентімен сипатталатын аз кедергі күшін ескеру қажет.
 уақыт
аралығында пайда болатын айнымалы
таңбалы импульстің әсерінен туатын
тербелісті, өткендегіге ұқсас жолмен
зерттейміз.
уақыт
аралығында пайда болатын айнымалы
таңбалы импульстің әсерінен туатын
тербелісті, өткендегіге ұқсас жолмен
зерттейміз.
Бұл жағдай үшін жүйе қозғалысы мына теңдеумен анықталады:
 (5.6.25)
(5.6.25)

 уақыт
мезетіндегі санаулы импульс үшін осы
теңдеуді мына түрде бейнелеуге болады:
уақыт
мезетіндегі санаулы импульс үшін осы
теңдеуді мына түрде бейнелеуге болады:
 (5.6.26)
(5.6.26)
Егер
импульс саны
 ,
онда (5.6.26) теңдеуі мына түрге ие болады:
,
онда (5.6.26) теңдеуі мына түрге ие болады:

 (5.6.27)
(5.6.27)
Санаулы импульстер үшін және өшу коэффициенті n=0 болғанда (5.6.26) теңдеуі бойынша түрдегі анықталмаушылықты аламыз. Осы анықталмушылықты жалпы тәртіп бойынша ашып, мынаны аламыз:
 (5.6.26)
(5.6.26)
32-суретте импульс саны s өсуімен қатар тербелістің артуын көрсететін график көрсетілген.
