Вычисление скалярного произведения
Задача
№ 1.
Найти скалярное произведение векторов
,
.
Решение.
Поскольку
векторы заданы в координатной форме,
используем для вычисления произведения
следующее соотношение
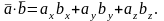В нашем случае
Задача
№ 2.
Определить угол между векторами
и
.
Решение. Используем для вычисления угла между векторами соотношение
Далее
Задача
№ 3.
Векторы
и
взаимно перпендикулярны; вектор
образует с ним углы, равные
;
зная, что
,
вычислить:
1)
.
Решение.
1)
.
10. Задачи на ортогональность векторов.
Задача № 1. Дано, что а=3, b=5. Определить, при каком значении векторы а+ b, а- b будут взаимно перпендикулярны.
Решение.
П
о
признаку перпендикулярности двух
векторов
П
реобразуем
левую часть последнего равенства
Задача № 2. Доказать, что диагонали ромба взаимно перпендикулярны.
Решение.
Рассмотрим
ромб. Составим скалярное произведение
вектора
на вектор
:
.
Но если скалярное произведение двух
ненулевых векторов
и
равно нулю, то эти векторы взаимно
перпендикулярны. Таким образом, доказано
утверждение: диагонали ромба взаимно
перпендикулярны.
11. Вычисление векторного произведения.
Задача
№ 1.
(Типовая)
Векторы
и
образуют угол
.
Зная, что
,
найти
.
Указание. При решении используется выражение через длины векторов и синус угла между ними из определения векторного произведения.
Задача
№ 2.
(Типовая)
Найти
,
если
.
Указание. С
помощью скалярного произведения
находится косинус
,
а затем, из основного тригонометрического
тождества – синус; и, воспользовавшись
определением векторного произведения,
находим
.
Задача
№ 3.(Типовая)
Найти
векторное произведение векторов
,
.
Решение. Поскольку векторы заданы в координатной форме, используем для вычисления вектоного произведения следующее соотношение
Задача № 4.(Типовая) Найти площадь параллелограмма, построенного на векторах а=6i+3j-2k и b=3i-2j+6k.
Решение. Вычислим векторное произведение векторов a и b.
Известно, что модуль векторного произведения равен площади параллелограмма, построенного на этих векторах, как на сторонах. Поэтому вычисляем модуль этого вектора.
Задача решена.
Задача № 5. Вычислить площадь треугольника с вершинами А(1,1,1,); B(2,3,4); C(4,3,2).
Решение.
Находим векторы
Площадь треугольника ABC равна половине площади параллелограмма, построенного на этих векторах как на сторонах.
Находим модуль вектора, равный площади параллелограмма.
Задача
№ 6. Вычислить
площадь параллелограмма, построенного
на векторах а+3
b
и 3а+b,
если
и угол между этими векторами равен 300.
Решение. Учитывая, что площадь параллелограмма равна векторному произведению векторов, имеем
Таким
образом, площадь искомого параллелограмма
будет равна
12. Вычисление смешанного произведения векторов.
Задача
№ 1.
(Типовая)
Найти
смешанное произведение векторов
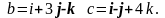
Решение. Смешанное произведение векторов, заданных своими координатами, определяется соотношением
Подставим сюда данные из нашей задачи
