1. Вычисление определителей второго и третьего порядка
Задача №1 Вычислить определители 2-го порядка
Решение.
а)
в)
г)
е)
ж)
Задача №4 Вычислить определители третьего порядка
Решение.
Вычтем из первой строки третью, а затем в полученном результате последовательно из второй и третьей строки вычитаем первую.
.
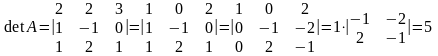4) раскрываем определитель по первому столбцу
5)
7)
11)
Вычитаем из первого столбцы второй и заменяем в третьем столбце cos2, cos2 и cos2 по формуле косинуса двойного угла.
Если затем из третьего столбца вычесть первый, он превращается в нуль и, следовательно весь определитель будет равен нулю.
19) Прибавим ко второй строке первую, а затем к третьей первую.
2. Разложение определителей по строке (столбцу)
Задача №1. Вычислить алгебраические дополнения определителя
.
Решение.
Задача №5. Решить уравнение:
а)
;
б)
Решение.
а) Раскрываем определитель по правилу треугольника.
.
Раскрываем скобки в выражении в квадратных скобках.
.
.
.
.
б)
.
.
.
.
.
.
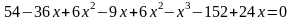Поделив этот многочлен на (х+2), находим
.
Откуда,
находим:
.
2. Действия с матрицами
Задача № 1. Пусть
.
Найти
.
Решение. Применяем операции сложения матриц и умножения матрицы на число:
.
.
Задача № 2. Вычислить произведение матриц второго порядка:
Решение. По правилу умножения матриц
Задача № 3. Вычислить произведение матриц (AB) и (BA).
.
Решение. По правилу умножения матриц
Поменяем местами матрицы и снова вычислим их произведение
Полученный результат подтверждает, что от перестановки сомножителей произведение матриц изменяется.
Задача № 4 . Найти обратную матрицу для матрицы
Решение. Найдем определитель матрицы, раскрывая его разложением по элементам второго столбца (т.к. а23=0).
Так как detA0, то обратная матрица существует. Подсчитаем алгебраические дополнения
Запишем присоединенную матрицу
Так
как
,
то получаем следующий результат
Проверим
полученный результат. Известно, что
,
тогда
3. Решение матричных уравнений.
Задача
№ 1.
Найти матрицу из уравнения
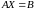, где
,
.
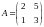Решение.
Если
умножим обе части уравнения слева на
матрицу
,
то получим
,
или
,
так как
,
.
Производя
необходимые вычисления, найдем, что
,
следовательно,
.
Задача № 2. Решить матричное уравнение
.
Решение. Имеем уравнение вида , решение которого , где
,
.
Найдем
обратную матрицу:
.
Сначала находим определитель
:
.
Для определения присоединенной матрицы вычисляем алгебраические дополнения всех элементов:
,
получаем
.
Находим решение матричного уравнения:
.
4. Определение ранга матрицы.
Задача № 1. Найти ранг матрицы
A=
Решение. Вычтем из первой третью, из второй - первую и из четвертой строки - вторую
.
Умножим первую строку на (-1) и сложим ее со второй и четвертой строками. Затем умножим первую строку на (-0,5) и сложим с третьей.
Умножим вторую строку на (-1) и сложим ее м третьей и четвертой.
~
~
Поменяем местами третью и четвертую строки
.
Получена
матрица ступенчатого вида, эквивалентная
исходной. Количество ненулевых строк
равно 3, значит ранг матрицы равен
.
Задача № 2. Найти ранг матрицы
Решение. Умножим вторую строку на (-1) и сложим ее с первой и четвертой
Умножим первую строку на (-1) и сложим ее с третьей
.
.