Список литературы
Кильчевский Н.А. Курс теоретической механики, т. 1 (кинематика, статика, динамика точки). – М.: Наука, 1977. – 480 с.
Маркеев А.П. Теоретическая механика. – М.: Наука, 1990. – 416 с.
Мещерский И.В. Сборник задач по теоретической механике: Учебное пособие. – 36-е изд., исправл. / Под ред. Н.В. Бутенина, А.И. Лурье, Д.Р. Меркина. – М.: Наука, 1986. – 448 с.
Ольховский И.И. Курс теоретической механики для физиков. – М.: Наука, 1970. – 447 с.
1
Запись
следует читать: «косинус угла между
векторами
и
».
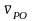
2 2 Вектор - это тот же вектор , только заданный в системе координат Oxyz.
3 3 Матрицей, обратной A, называют матрицу A-1, такую, что A-1A=E, где E – единичная матрица. Матрица AT - транспонированная, в которой строки и столбцы меняются местами.
4 4 В целях сокращения записей формул в технической литературе используются обозначения:
, .
5 5 Кососимметрической называют такую матрицу B, для которой справедливо равенство: BT = -B.
6 6 В данном случае осестремительное ускорение равно нормальному, а вращательное ускорение– тангенциальному.
7 7 Обозначение читается так: «скорость точки P относительно точки O».
8 8 Входными в механике называются звенья механизма, через которые к нему поступает механическая энергия от двигателей. Законы движения входных звеньев, как правило, известны.
9 9 Выходными звеньями называются звенья механизма, совершающие требуемые технологические движения. Вообще, любой механизм можно рассматривать как преобразователь механической энергии двигателей в механическую энергию требуемых технологических движений выходных звеньев.
10 10 Уравнения (3) – общая форма записи линейных относительно скоростей неголономных связей. Например, неголономная связь из предыдущей задачи в общей форме будет иметь вид: , где , .