Оглавление
1 Постановка задачи линейного программирования, условия существования и свойства оптимальных решений задачи линейного программирования 3
1.1 Постановка задачи линейного программирования 3
1.2 Стандартная задача ЛП 3
1.3 Каноническая задача ЛП 4
1.4 Общая задача ЛП 4
1.5 Двойственная задача линейного программирования. 5
2 Понятия о системном подходе, системном анализе, его основные методологические принципы 7
2.1 С сайта (http://b-i.narod.ru/sys.htm) 7
2.2 По Вентциль 10
2.2.1 Схема операционного проекта 10
3 Системы и закономерности их функционирования и развития, управляемость, достижимость, устойчивость 13
4 Классификация моделей систем (статические, динамические, концептуальные, топологические, формализованные (процедуры формализации моделей систем), информационные, логико-лингвистические, семантические, теоретико-множественные) 15
5 Постановка и классификация задач принятия решений, этапы решения задач 17
6 Допустимое множество и целевая функция в задачах математического программирования, классификация, формы записи 20
6.1 Классификация задач математического программирования 20
7 Основные виды иерархических структур. Модель функционирования иерархической системы 22
7.1 Из интернетов 22
7.2 По википедии 33
7.2.1 Структурная часть иерархической модели 34
7.2.2 Управляющая часть иерархической модели 34
7.3 По лекциям из интернетов 35
8 Основные понятия теории иерархических систем и их формализация 41
8.1 Координация 41
8.2 Декомпозиция 43
8.3 Агрегация 44
9 Классификация вычислительных задач по степени сложности. Классы сложности задач P и NP. NP сложные и NP трудные задачи 46
9.1 По книге Системы искусственного интеллекта 46
9.2 По интернетам 63
9.2.1 Классы задач в зависимости от их трудности 63
9.3 По википедии 63
9.3.1 Классы сложности 63
9.3.2 Класс P 63
9.3.3 Класс NP 63
9.3.4 Проблема равенства классов P и NP 64
10 Метод динамического программирования. Принцип оптимальности Беллмана 65
11 Методы и задачи дискретного и целочисленного программирования. Метод ветвей и границ 69
12 Решение задачи линейного программирования симплекс-методом 70
12.1 Симплекс-таблица, стандартный алгоритм симплекс-преобразования 71
12.2 Алгоритм отыскания опорного решения задачи ЛП 73
12.3 Алгоритм отыскания оптимального решения задачи ЛП 74
12.4 Схема алгоритмов решения задач ЛП 75
12.5 Алгоритм получения первого базисного решения с использованием симплекс — процедуры (метод искусственного базиса) 78
12.6 Вырожденная задача ЛП 80
Постановка задачи линейного программирования, условия существования и свойства оптимальных решений задачи линейного программирования
Постановка задачи линейного программирования
Основная задача линейного программирования выглядит следующим образом.
Дана система m линейных уравнений с n неизвестными:
(3.1.1)
где все неизвестные могут принимать только неотрицательные значения:
(3.1.2)
и линейная функция от тех же переменных
(3.1.3)
называемая целевой функцией.
Требуется среди всех решений системы уравнений (3.1.1) найти такое неотрицательное решение, при котором целевая функция (3.1.3) принимает наибольшее возможное значение.
Любое неотрицательное решение системы
уравнений (3.1.1) называют допустимым
решением, а то допустимое решение, при
котором целевая функция (3.1.3) принимает
наименьшее значение, называют оптимальным
80 решением задачи линейного программирования
(3.1.1)—(3.1.3). Кратко задачу формулируют
так: найти вектор
,
минимизирующий целевую функцию (3.1.3)
при линейных ограничениях (3.1.1) и (3.1.2).
Стандартная задача лп
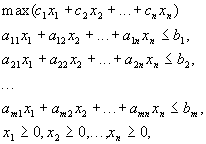
или, в матричной записи,
где 
—
матрица коэффициентов. Вектор 
называется
вектором коэффициентов линейной
формы, 
—
вектором ограничений.
Стандартная задача важна ввиду наличия большого числа прикладных моделей, сводящихся наиболее естественным образом к этому классу задач ЛП.
Каноническая задача лп
или, в матричной записи,
Основные вычислительные схемы решения задач ЛП разработаны именно для канонической задачи.
Общая задача лп
В этой задачи часть ограничений носит характер неравенств, а часть является уравнениями. Кроме того, не на все переменные наложено условие неотрицательности:
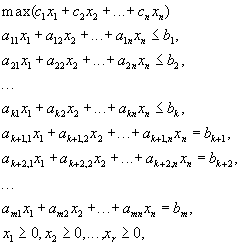
Здесь
.
Ясно, что стандартная задача получается
как частный случай общей при 
;
каноническая — при 
.
Все три перечисленные задачи эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных.
При изучении задач ЛП сложилась
определенная терминалогия. Линейная
форма 
,
подлежащая максимизации (или минимизации)
, называется целевой функцией. Вектор 
,
удовлетворяющий всем ограничениям
задачи ЛП, называется допустимым
вектором, или планом. Задача ЛП, для
которой существуют допустимые векторы,
называется допустимой задачей. Допустимый
вектор 
,
доставляющий наибольшее значение
целевой функции по сравнению с любым
другим допустимым вектором 
,
т.е. 
,
называется решением задачи, или
оптимальным планом. Максимальное
значение 
целевой
функции называется значением задачи.
Двойственная задача линейного программирования.
Рассмотрим задачу ЛП
(1)
или, в матричной записи,
(2)
Задачей, двойственной к (1) (двойственной
задачей), называется задача ЛП
от 
переменных 
вида
(3)
или, в матричной записи,
(4)
где 
.
Правила построения задачи (3) по форме
записи задачи (1) таковы: в задаче (3)
переменных 
столько
же, сколько строк в матрице 
задачи
(1). Матрица ограничений в (3) —
транспортированная матрица
.
Вектор правой части ограничений в (3)
служит вектором коэффициентов
максимизируемой линейной форме в (1),
при этом знаки неравенств меняются на
равенство. Наоборот, в качестве целевой
функции в (3) выступает линейная форма,
коэффициентами которой задаются вектором
правой части ограничений задачи (1), при
этом максимизация меняется на минимизацию.
На двойственные переменные
накладывается
условие неотрицательности. Задача (1),
в отличии от двойственной задачи (3)
называется прямой.
Теорема двойственности. Если взаимодвойственные задачи (2), (4) допустимы, то они обе имеют решение и одинаковое значение.
Теорема равновесия. Пусть 
—
оптимальные планы прямой (1) и двойственной
(3) задач соответственно. Тогда если 
то
