9. Потенциальная энергия деформации пластин.
10. Вариационные методы расчета пластин.
Точные аналитические решения получить невозможно. Поэтому применяют вариационне методы, которые позволяют решать задачи теории упругости в приблежении.
При этом не точно удовлетворяются дифференциальные уравнения и граничные условия.
В основе – вариационные принципы (например, принцип возможных перемещений, принцип Лагранжа.)
В расчете пластин вариац.методы позволяют получить приближенное решение для прогиба пластины с точностью , достаточной для практического применения.
При этом искомая функция задаётся виде уравнения, соответствующего характеру изогнутой срединной поверхности пластины и удовлетворяющая граничные условия.
Это уравнения должно содержать неизвестный коэффициент одной переменной для определения которой принимается один из варифц.принципов.
Такой подход сводит диф.уравнения к решению линейных уравнений.
Функция прогибов:
W(x,y) ∑_(k=1)^m ∑_(l=1)^n▒akl φkl (x,y), где к – 1,2,3..m . l=1,2,3..n
В этом выражении функция φkl должна быть линейно независимая удовлетворять кинематическим граничным условиям. Они задаются в начале расчета и называются аппроксимарующими.
Коэффициент аkl является постоянным числом и должен быть определен
11. Расчет пластин методом Ритцы-Тимошенко
Основан на теореме Дирихле-Лагранжа, в котором утверждается: потенциальная энергия упругого тела в состоянии устойчивого равновесия имеет минимальное значение.
1
-безразличное
2 неустойчивое
3- усточйчивое
Для этого нужно составлять выражения для потенциальной энергии деформации пластины U и работы внешних сил А.
П= U-А (1)
При задании прогибов в виде (1), полная потенциальная энергия пластинки является квадратичной функцией параметров аkl :
П=П(аkl2)
Для выполнения условия минимума полной потенциальной энергии пластины, надо составить частные производные от П по всем параметрам аkl
П/
аkl
=0
(2)
Уравнение (2) позволяет получить систему линейных алгебраических уравнений относительно аkl. Найдя эти параметры и подставив в (1), получим приближенное решение задачи.
12. Расчет пластин методом Бубнова-Галеркина.
13. Расчет пластин методом Власова.
14. Расчет пластин методом конечных разностей.
15. Расчет пластин МКЭ.
1 этап. Составление КЭ схемы:
a) выбор типа КЭ ( по геометрии, виду апроксимации ……..)
б) Разбивка области на КЭ с номерами узлов и элем.
В) Описание заданных узловых нагрузок
2 этап. Формирование матриц жёсткости и вектора узловых сил.
а) Составление элементов МЖ и ВН в локальной системе координат
б) Преобразование элементов МЖ и ВН из локальной в глобальную систему координат
3 этап. Учёт заданных статических и кинематических граничных условий.
16. Цилиндрический изгиб пластин.
Ц.И.- это такой вид деформации пластинки, когда ее срединная плоскость искривляется по цилиндрической поверхности. При этом кривизная срединной поверхности по одному направлению равна 0.
Ц.И наблюдается в достаточно длинной прямоугольной пластинке при действии поперечной нагрузки, которая не изменяется вдоль длинной стороны р=const.
Если в>2а, изогнутую срединную поверхность большей части пластины, исключая торцы у=0, у=в, можно считать цилиндрической поверхностью с образующей параллельной длинной стороне.
D
= q(x)
D-
цилиндрическая жесткость
ЦИ пластинки можно рассматривать как изгиб множества балок-полок прямоугольного поперечного сечения единичной ширины, вырезанной из пластины в направлении оси Х.
Расчет производится методами сопромата.
ЦИ имеют отличий от изгиба балок. Оно выявляется в том, что при изгибе балок кк поперечные деформации ничем не теснены и могут происходить спокоцно, что приводит к изменению формы поперечного сечения при чистом изгибе.
Здесь
уменьшается ширина сечения в зоне
действия растягивающих напряжений и
увеличение ее в зоне сжимающих напряжений
При ЦИ поперечные деформации выделенной полосы невозможны из за сопротивления соседних балок-полос.
Поперечные деформации εу=0 и норм.напряжения находятся:
σх=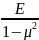
(εх
+μ
εу)
= -
w,
xx
σy=
(εy
+μ
εx)
= -
w,
xx
=μσх
Mx=-Dw,xx
My=-Dμw,xx=μ Mx
17. Основные уравнения расчета пластин в полярной системе координат.
18. Круглая пластина нагруженная концентрически.
19. Круглая пластина, нагруженная в центре силой.
20. Применение рядов Фурье в приложении к расчету пластин.