1. Основные понятия, гипотезы, принимаемые при расчете пластин и следствия из них.
Пластиной называется призматическое тело, высота которого мала по сравнению с размерами в плане.
Плоскость которая делит пластину пополам называется срединной.
Линия пересечения бок. Пов. Пластинки со сред назю контуром пластины.
1) Толстые – пластины при b/h < =8….10. Расчёт производят как массивный объект.
2) Тонкие – 8….10<=b/h<=80….100
А)Жёсткие –w/h<=0.2…..0.5
Б)Гибкие- w/h > 0.2….0.5, работая на изгиб как мембрана.
3)Мембраны – b/h>=80…..100. Работаю только по закреп краям контура. Сопр на изгиб малы.
I) Гипотеза прямых номарлей. Любой линейный элемент, нормальный к срединной плоскости пластинки, остаётся прямолинейным и нормальным к срединной поверхности в процессе изгиба и длина не измен.
II) Отсутствет давление между слоями пластинки – напряжение надавливания горизонтальных слоёв пластинки друг на друга (сигма z) опускаем по сравнению с уровнями напряжений (сигма х, сигма y) . ГИПОТЕЗЫ КИРГОФА-ЛЯВА.
III) Нерастяжимости срединной поверхности – при малых прогибах (w/h <= 0,2….0,5) в срединной поверхности отсутств деформации напряжения, сжатия и сдвига нейтральна.
2. Выражение перемещений и деформаций через прогибы пластины
Первое
допущение – длина перпендикуляра mn
не измен. Т.к.
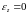и он не искривляется при изгибе (
)
------
----
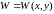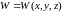
Ур-е говорит, что прогибы не зависят от Z и все точки принадлежат mn, получаем одинаковый прогиб.
Из
ур-я КОШИ -----
Интегрируя по Z получаем:
Пользуясь
гипотезой нерастяжимости срединной
плоскост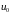и
и
при Z=0
равны 0.
Подставляя в ур-я получаем
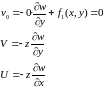
3. Напряжения в пластине и их выражения через прогибы
Формулы закона Гука
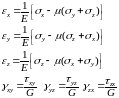
Из первой и второй гипотезы:
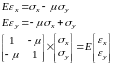
Применим
правило Крамера
-определитель
из коэффициентов при неизвестных
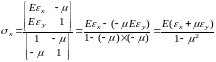
Определим напряжения заменив перемещения на дифференциальные (2,4) уравнения через прогибы
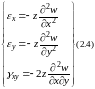
4. Усилия в пластинке и их выражения через прогибы
Выясним какое усилие возникнет в сечении пластинки нормальной к ее срединной поверхности:
Определим приходящуюся на единице ширины сечения продольную силу N. Она равна сумме проекций на ось Х
Нормальной силы в этом сечении не возникает. (сука а нахуя я тогда все это писал)
Найдем изгибающий момент:
-
цилиндрическая жесткость при изгибе.
Поперечная сила:
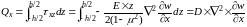
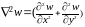
Сдвигающая сила
Погонный крутящий момент:
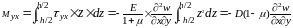
Аналогично найдем усилия, действующие в сечении с нормалью у.
5. Выражение напряжений через усилия
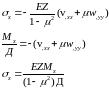
Нормальные напряжения при изгибе прямоугольной балки высотой h и шириной =1.
H-крутящий момент
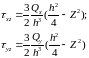
6. Уравнения равновесия элемента пластины
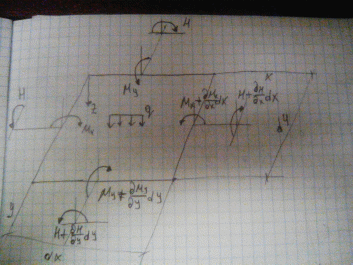
Спроекцируем все силы на ось Z.
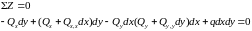
Приведя подобные члены:
Запишем
уравнение равновесия
относительной ОХ.
7. Дифференциальное уравнение изогнутой срединной поверхности пластины.
Исключая из второго и третьего уравнения равновесия поперечные силы получим:
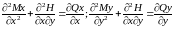
Подставляя полученные выражения в первое уравнения равновесия в первое уравнения равновесия, получим:
Это уравнение представляет собой дифференциально уравнение изогнутой срединной поверхности пластинки, его называют уравнением Софи Жермен-Лагранжа. С помощью него, использую граничные условия находит функции прогибов.