
- •Тема 1.Сводка и группировка статистических данных.
- •Тема 2: Абсолютные, относительные и средние величины. Показатели вариации.
- •Тема 3: Моменты распределения. Асимметрия и эксцесс.
- •Тема 4: Выравнивание вариационных рядов (построение теоретических распределений)
- •Тема 5. Выборочное наблюдение.
- •Тема 6. Изучение динамики общественных явлений. Ряды динамики.
- •Тема 7. Экономические индексы
- •Тема 8. Корреляционно-регрессионный анализ
Тема 5. Выборочное наблюдение.
Задача 15.
На предприятии, на котором работает 250 человек, было проведено обследование размера заработной платы. Результаты в таблице:
Группа рабочих |
Кол-во, чел. |
Сред.з/п, руб |
Сред.кв.отклонение |
Мужчины |
7 |
610 |
4 |
Женщины |
3 |
770 |
2 |
Рассчитать общую среднюю зарплату по выборочным данным. С вероятностью 0,997 определить доверительные пределы средней зарплаты в генеральной совокупности и среднюю ошибку выборочной средней.
Рассчитаем общую среднюю зарплату в выборочной совокупности. Все расчёты оформим в таблицу.
Группа рабочих |
Кол-во, чел.(fi) |
Сред.з/п, руб(xi) |
xi*fi |
Xср |
Xi-Xср |
(Xi-Xср)^2 |
(Xi-Xср)^2*f |
дисперсия |
Мужчины |
7 |
610 |
4270 |
658 |
-48 |
2304 |
16128 |
5376 |
Женщины |
3 |
770 |
2310 |
|
112 |
12544 |
37632 |
|
итого |
10 |
|
6580 |
|
|
|
53760 |
|
Среднее рассчитывается по формуле:
Xср = 6580/10=658
Рассчитаем дисперсию выборочной совокупности.

^2= 53760/10=5376
Найдем ошибку выборки по формуле:

Чтобы найти t при вероятности P=0.997,обратимся к таблице.
Значение коэффициента доверия в зависимости от вероятности
t |
P |
1,0 |
0,683 |
1,5 |
0,866 |
1,96 |
0,950 |
2,0 |
0,954 |
2,5 |
0,988 |
2,58 |
0,990 |
3,0 |
0,997 |
3,5 |
0,999 |
^2=5376;
n=7+3=10;
N=250
![]() =
3*√(5376/10)(1-(10/250)=3*√(537,6)(0,96) = 3*√516,096 =
=3*22,72=68,15
=
3*√(5376/10)(1-(10/250)=3*√(537,6)(0,96) = 3*√516,096 =
=3*22,72=68,15
Определим
пределы .Так как,
![]() ,
то
,
то
![]() =
658 ± 68,15, то есть генеральная средняя
находится в пределах 658-68,15<
<658+68,15;
589,85<
<726,15
=
658 ± 68,15, то есть генеральная средняя
находится в пределах 658-68,15<
<658+68,15;
589,85<
<726,15
В
результате, с вероятностью 0,997 можно
утверждать, что средняя зарплата на
предприятии находится в пределах 589,85
˂ ![]() ˂726,15
рублей.
˂726,15
рублей.
Тема 6. Изучение динамики общественных явлений. Ряды динамики.
Задача 65.
На основе данных о производстве стиральных машин фирмой за 15 месяцев 2008-2009гг. произведите сглаживание ряда методом трех- и четырехчленной скользящей средней.
месяцы |
Стир. машины, тыс. шт. |
3-членные скользящие суммы |
3-членные скользящие средние |
4-членные скользящие суммы |
4-членные скользящие средние (нецентрир.) |
4-членные скользящие средние |
1 |
155 |
- |
- |
- |
- |
- |
2 |
163 |
- |
161,67 |
- |
154 |
- |
3 |
167 |
485 |
153,67 |
- |
154,75 |
154,375 |
4 |
131 |
461 |
152,00 |
616 |
150,75 |
152,75 |
5 |
158 |
456 |
145,33 |
619 |
141,5 |
146,125 |
6 |
147 |
436 |
145,00 |
603 |
145 |
143,25 |
7 |
130 |
435 |
140,67 |
566 |
137,5 |
141,25 |
8 |
145 |
422 |
134,33 |
580 |
135,75 |
136,625 |
9 |
128 |
403 |
137,67 |
550 |
143 |
139,375 |
10 |
140 |
413 |
142,33 |
543 |
146,75 |
144,875 |
11 |
159 |
427 |
153,00 |
572 |
151,5 |
149,125 |
12 |
160 |
459 |
155,33 |
587 |
154 |
152,75 |
13 |
147 |
466 |
152,33 |
606 |
155,5 |
154,75 |
14 |
150 |
457 |
154,00 |
616 |
- |
- |
15 |
165 |
462 |
- |
622 |
- |
- |
Взяв
данные за первые три месяца, исчислим
трехчленные суммы, а затем скользящую
среднюю:
 ;
;
 ;
;
 ;
;
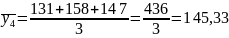 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Четырехчленные скользящие средние (нецентрированные) находят подобным способом что и трехчленные.
 ;
;
 и так далее.
(Посчитано с помощью программы Excel).
и так далее.
(Посчитано с помощью программы Excel).
Затем находим центрированные скользящие средние следующим образом:

![]() и так далее.
(Посчитано в таблице с помощью программы
Excel)
и так далее.
(Посчитано в таблице с помощью программы
Excel)
