Лекция № 2. Графический метод решения задач линейного программирования
2.1. Задача с двумя переменными
Графическим методом могут быть решены задачи линейного программирования с двумя переменными и некоторые задачи с большим числом переменных при выполнении определенных условий.
Задача линейного программирования с двумя переменными должна иметь систему ограничений, представляющую собой систему неравенств. Неравенства могут быть как вида " ", так и " ". Условия неотрицательности могут отсутствовать. Математическая модель должна иметь вид
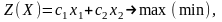(2.1)
(2.2)
.
Метод решения данной задачи основывается на возможности графического изображения области допустимых решений (ОДР) и нахождения в этой области оптимального решения. Для обоснования метода докажем две теоремы.
Теорема
2.1. О виде
области решений линейного неравенства.
Областью решений линейного неравенства
является одна из двух полуплоскостей,
на которые разбивает всю координатную
плоскость
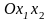прямая
,
соответствующая этому неравенству.
Доказательство.
В системе координат О
построим прямую
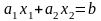(L)
и ее нормаль
(рис. 2.1).
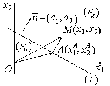
Рис. 2.1
Прямая
(L)
разбивает плоскость О
на две полуплоскости: верхнюю (
),
соответствующую направлению нормали
,
и нижнюю (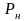
).
Пусть произвольно выбранная точка М(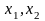
)
принадлежит (
),
ее проекцией на прямую (L)
является точка
.
Вектор
.
Координаты векторов
и
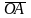совпадают с координатами точек М
и А,
т. е.
=
(
),
.
Вектор
коллинеарен вектору
,
поэтому
=
,
где
некоторое число. Найдем скалярное
произведение
.
Запишем это равенство через координаты
векторов
.
Так как точка А
принадлежит прямой (L),
то
,
получаем
.
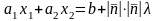Отсюда следует, что если >0,
т. е. (
),
то
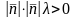и тогда
.
Если же <0,
(
),
то
и
.
Пример
2.1. Найти
область решений неравенства
.
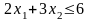Решение.
Строим прямую
(рис. 2.2).
Р
ис.
2.2
Чтобы определить какая из двух полуплоскостей является областью решений, выбираем произвольно "пробную" точку, не лежащую на прямой, и подставляем ее координаты в неравенство. Если неравенство выполняется, то область, содержащая эту "пробную" точку, является областью решений. Если же неравенство не выполняется, то областью решений будет полуплоскость, не содержащая "пробную" точку.
В рассматриваемом примере в качестве "пробной" точки возьмем О(0, 0). Подставляем координаты этой точки в неравенство, получаем 2 0 + 3 0 6 0 6, следовательно, областью решений является полуплоскость, содержащая начало координат. Этот факт отмечаем на рисунке стрелками.
В общем случае, когда система ограничений состоит из нескольких неравенств, область допустимых решений (ОДР) находят как пересечение полуплоскостей – решений каждого из неравенств-ограничений. ОДР может быть пустым множеством, многоугольником и многоугольным множеством (многоугольником, неограниченным с одной из сторон). Для нахождения среди допустимых решений оптимального используют линии уровня.
Линией
уровня
называется прямая, в точках которой
целевая функция постоянна Z(X)
=
.
Уравнение линий уровня
, с = const.
Теорема 2.2. Об изменении значений функции. Значения целевой функции в точках линий уровня возрастают, если линии уровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении.
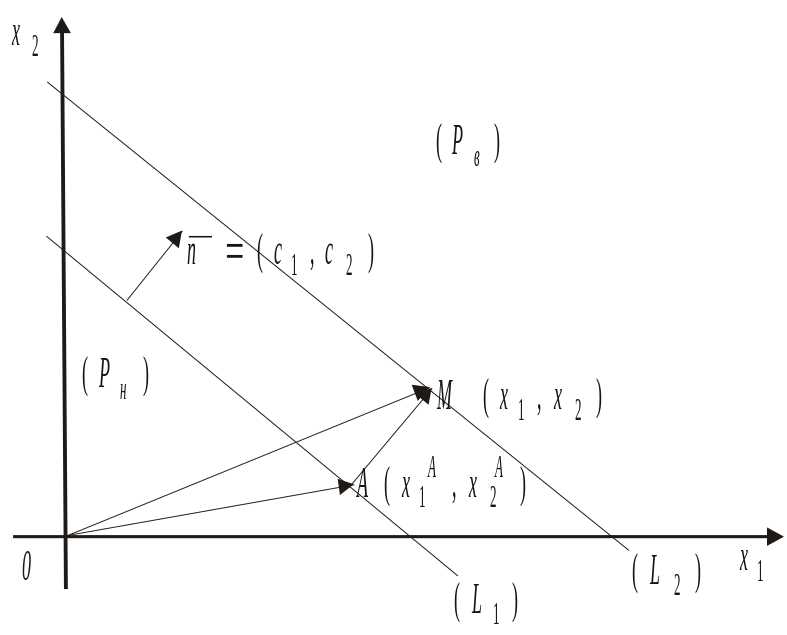
Рис. 2.3
Доказательство.
Пусть целевая
функция задачи линейного программирования
имеет вид Z(X)
=
.
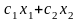В системе координат О
построим две линии уровня (L
)
и (L
)
(рис. 2.3). Их общая нормаль
.
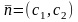Пусть точка М(
)
(L
),
а точка
(L
)
является проекцией М
на (L
).
Вектор
,
=
(
),
.
Так как
коллинеарен вектору
,
то вектор
=
,
где
число. Скалярное произведение
.
Используя координаты векторов
и
,
можно записать
.
Так как
,
,
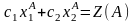то
.
Отсюда
получаем следующие выводы: 1) если линия
уровня перемещается в направлении
нормали
из положения (L
)
к (L
),
то
> 0 и, следовательно,
;
2) если же линия уровня перемещается в
направлении противоположном направлению
нормали
из положения (L
)
к (L
),
то
< 0 и, следовательно,
.
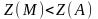Таким образом, если задача линейного программирования на максимум, то для нахождения оптимального решения линии уровня надо перемещать по ОДР в направлении нормали, а в задаче на минимум наоборот – в противоположном направлении. Для нахождения оптимального решения задачи необходимо использовать опорную прямую.
Опорной прямой называется линия уровня, относительно которой ОДР находится в одной из полуплоскостей и которая имеет хотя бы одну общую точку с ОДР. Если ОДР является замкнутым многоугольником, то независимо от вида целевой функции имеется две опорных прямых. Если же ОДР – многоугольное множество (незамкнутый многоугольник), то в зависимости от направления нормали линий уровня ОДР может иметь как две, так и одну опорную прямую.
Алгоритм графического метода решения задач линейного программирования с двумя переменными заключается в следующем.
1. Строится область допустимых решений.
2. Если область допустимых решений является пустым множеством, то ввиду несовместности системы ограничений задача не имеет решения.
3.
Если область допустимых решений – это
непустое множество, то строится нормаль
линий уровня
и одна из линий уровня, имеющая общие
точки с этой областью.
4. Линия уровня перемещается до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум – в противоположном.
5. Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
6. Если задача линейного программирования имеет оптимальное решение, то для его нахождения решаются совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычисляется значение целевой функции на этих решениях.
Пример 2.2. Решить задачу линейного программирования
Рис. 2.4
Решение.
Изобразим на плоскости систему координат
(рис. 2.4) и построим граничные прямые
области допустимых решений.
Прямые, ограничивающие ОДР:
Область
допустимых решений определяется
многоугольником ОАВСD.
Для линий уровня
(с
= const) строим нормальный вектор
.
Перпендикулярно вектору
построим одну из линий уровня (на
рисунке она проходит через начало
координат). Так как задача на максимум,
то перемещаем ее в направлении вектора
до опорной прямой. На рисунке видно,
что опорная прямая проходит через точку
B,
являющуюся точкой пересечения первой
и второй граничных прямых,
.
Для определения координат точки В
решаем систему уравнений
Получаем
=
3,
=
6. Данному оптимальному решению
X
= (3; 6)
соответствует максимальное значение
целевой функции
max
Z(X)
= 2
3 + 4
6 =30.
Ответ: max Z(X) = 30 при X = (3; 6).
Пример 2.3 Решить задачу линейного программирования.
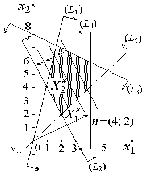
Рис. 2.5
Решение.
Строим область допустимых решений,
нормаль линий уровня
и одну из линий уровня, имеющую общие
точки с этой областью (рис. 2.5). Перемещаем
линию уровня в направлении противоположном
направлению нормали
,
так как решается задача на отыскание
минимума функции. Нормаль линии уровня
и нормаль
=
(2; 1) второй граничной прямой, в направлении
которой перемещаются линии уровня,
параллельны, так как их координаты
пропорциональны 4/2 = 2/1. Следовательно,
опорная прямая совпадает со второй
граничной прямой области допустимых
решений, проходит через две угловые
точки этой области
и
.
Задача имеет бесконечное множество
оптимальных решений, являющихся точками
отрезка
.
Находим точки
,
,
решая соответствующие системы уравнений.
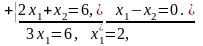
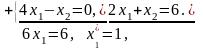
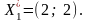
Вычисляем
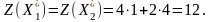
Ответ:
при
Пример 2.4. Решить задачу линейного программирования.
Рис. 2.6
Прямые, ограничивающие ОДР:
Решение.
Строим область допустимых решений,
нормаль
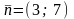и одну из линий уровня (рис. 2.6). В данной
задаче необходимо найти максимум
целевой функции, поэтому линию уровня
перемещаем в направлении нормали. Ввиду
того, что в этом направлении область
допустимых решений не ограничена, линия
уровня уходит в бесконечность. Задача
не имеет решения по причине неограниченности
целевой функции.
Ответ:
.
Пример 2.5. Решить задачу линейного программирования.
Рис. 2.7
Решение. Строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств (рис. 2.7). Область допустимых решений задачи – пустое множество. Задача не имеет решения ввиду несовместности системы ограничений.
Ответ: система ограничений несовместна.