
- •Лекция №1. Математические модели задач линейного программирования
- •1.1. Математические модели общих задач математического и линейного программирования
- •1.2. Примеры составления математических моделей задач линейного программирования
- •1.3. Каноническая форма задачи линейного программирования
- •1.4. Приведение общей задачи линейного программирования к канонической форме
- •Лекция № 2. Графический метод решения задач линейного программирования
- •2.1. Задача с двумя переменными
- •Лекция №3 графический метод решения задач линейного программирования Графический метод решения задач линейного программирования с n переменными
- •Задания для самостоятельного решения
- •Лекция№4. Свойства решений задач линейного программирования
- •4.1. Многоугольники и многогранники
- •4.2. Теорема о виде области допустимых решений задачи линейного программирования
- •4.3. Теорема об экстремуме целевой функции
- •4.4. Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
- •Лекция№5-6. Симплексный метод решения задач линейного программирования
- •5.1. Нахождение начального опорного решения и переход к новому опорному решению
- •5.2. Преобразование целевой функции при переходе от одного опорного решения к другому
- •5.3. Улучшение опорного решения
- •5.4. Алгоритм симплексного метода решения задач линейного программирования
- •Лекция №7. Метод искусственного базиса
- •Особенности алгоритма метода искусственного базиса
- •Лекция №8 теория двойственности Виды математических моделей двойственных задач
- •Симметричные пары двойственных задач
- •Несимметричные пары двойственных задач
- •Общие правила составления двойственных задач
- •Первая теорема двойственности
- •Вторая теорема двойственности
- •Лекция №9 Двойственный симплексный метод
- •Алгоритм двойственного симплексного метода
- •Лекция №10 транспортная задача линейного программирования
- •Текстовая формулировка транспортной задачи
- •Математическая модель транспортной задачи
- •Необходимое и достаточное условие разрешимости транспортной задачи
- •. Свойство системы ограничений транспортной задачи
- •Опорное решение транспортной задачи
- •Метод вычеркивания
- •Методы построения начального опорного решения. Метод северо-западного угла
- •Метод минимальной стоимости
- •Переход от одного опорного решения к другому
- •Означенный цикл
- •Распределительный метод
- •Лекция №11 Метод потенциалов
- •6.10. Особенности решения транспортных задач с неправильным балансом
- •Алгоритм решения транспортной задачи методом потенциалов
- •Транспортная задача с ограничениями на пропускную способность
- •Транспортная задача по критерию времени
- •Применение транспортной задачи для решения экономических задач Задача о размещении производства с учетом транспортных затрат
- •Задача о назначениях, или проблема выбора
- •Лекция №12 метод гомори решения задач целочисленного программирования
- •Лекция №13
- •Лекция №14 построение сетевых моделей
- •Методические рекомендации по построению сетевых моделей
- •Варианты задач для самостоятельного решения
- •Расчет и анализ сетевых моделей
- •Список литературы
- •Вопросы
Лекция №8 теория двойственности Виды математических моделей двойственных задач
Любой задаче линейного программирования (исходной или прямой) можно поставить в соответствие другую задачу, которая называется двойственной или сопряженной. Обе эти задачи образуют пару двойственных (или сопряженных) задач линейного программирования. Каждая из задач является двойственной к другой задаче рассматриваемой пары.
Рассмотрим составление двойственной задачи на примере задачи использования сырья.
Имеется
m
видов сырья в количестве
 ,
которые используются для изготовления
n
видов продукции. Известно: aij
– расход i-го
вида сырья на единицу j-й
продукции; сj
прибыль при реализации единицы j-го
вида продукции. Составить план выпуска
продукции, обеспечивающий максимальную
прибыль.
,
которые используются для изготовления
n
видов продукции. Известно: aij
– расход i-го
вида сырья на единицу j-й
продукции; сj
прибыль при реализации единицы j-го
вида продукции. Составить план выпуска
продукции, обеспечивающий максимальную
прибыль.
Математическая модель данной задачи имеет вид
 ,
(5.1)
,
(5.1)
 (5.2)
(5.2)
, j = 1, 2, . . . , n. (5.3)
Здесь , j = 1, 2, ..., n – объем производства j-го вида продукции.
Предположим,
что имеется второй производитель,
который хочет перекупить сырье. Составим
двойственную задачу, решение которой
позволяет определить условия продажи
сырья. Введем вектор оценок (цен) видов
сырья Y
= ( ).
Затраты на приобретение i-го
вида сырья в количестве
равны
).
Затраты на приобретение i-го
вида сырья в количестве
равны
 .
Второму производителю выгодно
минимизировать суммарные затраты на
приобретение всех видов сырья, поэтому
целевая функция имеет вид
.
Второму производителю выгодно
минимизировать суммарные затраты на
приобретение всех видов сырья, поэтому
целевая функция имеет вид
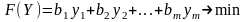 .
(5.4)
.
(5.4)
Первому производителю невыгодно продавать сырье, если суммарная стоимость всех видов сырья, расходуемых на каждое изделие j-й продукции
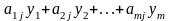 ,
,
меньше прибыли , получаемой при реализации этого изделия. Система ограничений задачи имеет вид
 (5.5)
(5.5)
Очевидно, что оценки видов сырья должны удовлетворять условиям неотрицательности
 ,
i
= 1, 2, ..., m.
(5.6)
,
i
= 1, 2, ..., m.
(5.6)
Таким образом, связь исходной и двойственной задач состоит в том, что коэффициенты целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные члены системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи, а матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи.
Рассмотренная пара задач относится к симметричным парам двойственных задач. В теории двойственности используются четыре пары двойственных задач (приведем их в матричной форме записи).
Исходная задача: Двойственная задача:
Симметричные пары двойственных задач
1.
Z(X)
= CX
max, F(Y)
=

min,
min,
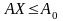 ,
,
 ,
(5.7)
,
(5.7)
.  .
.
2. Z(X) = CX min, F(Y) = max,
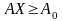 ,
,
 ,
(5.8)
,
(5.8)
. .
Несимметричные пары двойственных задач
3. Z(X) = CX max, F(Y) = min,
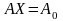 ,
.
(5.9)
,
.
(5.9)
.
4. Z(X) = CX min, F(Y) = max,
, . (5.10)
.
Здесь
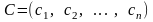 ,
,
 ,
,
 ,
,
,
,
,
,
