Лекция №1. Математические модели задач линейного программирования
1.1. Математические модели общих задач математического и линейного программирования
Основой решения экономических задач являются математические модели.
Математической моделью задачи называется совокупность математических соотношений, описывающих суть задачи.
Составление математической модели включает: выбор переменных задачи; составление системы ограничений; выбор целевой функции.
Переменными
задачи называются величины
,
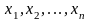которые полностью характеризуют
экономический процесс. Обычно их
объединяют в вектор
.
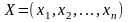Системой ограничений задачи называют совокупность уравнений и неравенств, описывающих ограниченность ресурсов рассматриваемой задачи.
Целевой функцией задачи называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.
В
общем случае математическая постановка
задачи
математического
программирования
формулируется следующим образом: найти
переменные задачи
),
обеспечивающие экстремум целевой
функции задачи
(1.1)
и удовлетворяющие системе ограничений, состоящей из уравнений и неравенств
(1.2)
Задача математического программирования называется задачей линейного программирования, если все функции (1.1), (1.2), входящие в математическую модель, линейные.
Задача линейного программирования в общем виде формулируется следующим образом: найти переменные задачи ), обеспечивающие экстремум целевой функции задачи
,
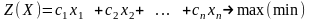(1.3)
удовлетворяющие системе ограничений
(1.4)
и условиям неотрицательности переменных
.
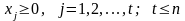(1.5)
В дальнейшем при записи математических моделей задач обычно приводятся только формулы вида (1.3), (1.4), (1.5) без словесной формулировки.
Допустимым решением (планом) задачи линейного программирования называется любой n-мерный вектор ), удовлетворяющий системе ограничений и условиям неотрицательности.
Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР).
Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.
1.2. Примеры составления математических моделей задач линейного программирования
Задача
использования ресурсов (сырья).
Для изготовления n
видов продукции используется m
видов
ресурсов (сырья). Известны:
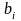(i
=
1, 2, ...,
m)
– запасы каждого i-го
вида ресурса (сырья);
,
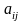(i
=
1, 2, ...,
m;
j
= 1, 2, 3, ..., n)
– затраты
каждого i-го
вида ресурса (сырья) на производство
единицы объема j-го
вида продукции;
(j
= 1, 2, 3, ..., n)
– прибыль
от реализации единицы объема j-го
вида продукции. Требуется составить
план производства продукции, который
обеспечивает максимум прибыли при
заданных ограничениях на ресурсы
(сырье).
Решение.
Введем вектор переменных задачи
),
где
(j
= 1, 2, ..., n)
– объем производства j-го
вида продукции. Затраты i-го
вида ресурса (сырья) на изготовление
данного объема
продукции равны
,
поэтому ограничение на использование
этого вида ресурса (сырья) имеет вид
.
Прибыль от реализации j-го
вида продукции равна
,
поэтому целевая функция
.
Математическая модель имеет вид
.
Задача
составления рациона.
Для полноценного откорма каждое животное
должно получать ежедневно m
питательных веществ в количествах не
менее
.
В рацион животных входят n
видов кормов. Известно:
(i
=
1, 2, ...,
m;
j
= 1, 2, 3, ..., n)
– содержание i-го
питательного вещества в единице j-го
вида корма;
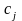(j
= 1, 2, 3, ..., n)
– стоимость единицы j-го
вида корма. Требуется составить суточный
рацион полноценного откорма животных,
обеспечивающий минимальные затраты.
Решение.
Введем переменные задачи
),
где
(j
= 1, 2,...,
n)
– объем
j-го
вида корма, входящего в суточный рацион.
Так как
– количество i-го
питательного вещества, содержащегося
в j-м
виде корма,
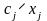– стоимость j-го
вида корма, входящего в суточный рацион,
то математическая модель имеет вид
.