7. Геометрия движения двух близких спутников в плоскости опорной орбиты.

Перегруппируем слагаемые первых двух уравнений системы (32):

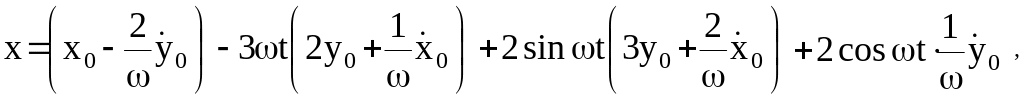
(33)

Введем линейную величину

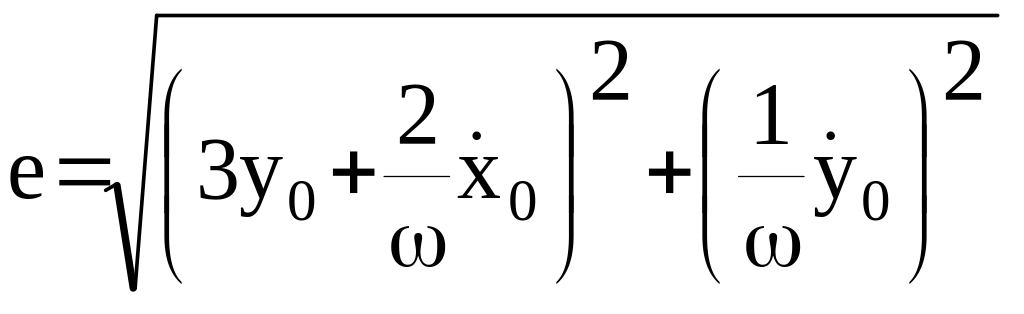
и угол такой, что

Т огда уравнения (33) принимают вид:

П оследние слагаемые правых частей каждого из уравнений системы

(35)

описывают движение по эллипсу, представленному на рисунке 3.

y

e

e

x

Рис.3.

Центр эллипса перемещается параллельно оси со скоростью

(36)

В начальный момент центр эллипса находится в точке с координатами

Из (35) следует, что величина полуоси эллипса вдоль оси абсцисс вдвое больше величины полуоси вдоль оси ординат, а движение по эллипсу происходит по направлению часовой стрелки, причем началом отсчета угла является луч, исходящий из центра эллипса в направлении, обратном направлению оси . Положение центра эллипса относительно опорной орбиты о пределяется знаком суммы . При центр эллипса в силу (36) не смещается с течением времени. При центр эллипса лежит выше опорной орбиты, т.к. из (37) следует, что в этом случае а скорость смещения центра вдоль оси отрицательна. При 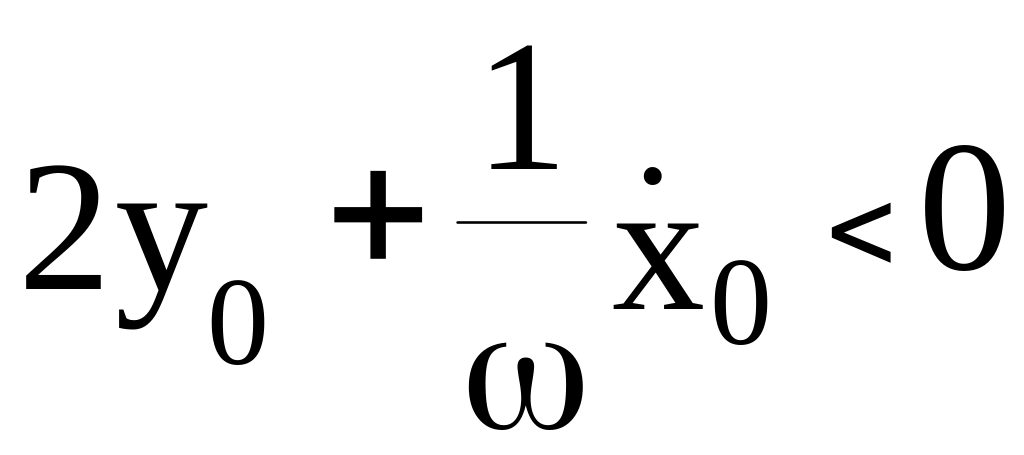центр эллипса находится ниже опорной орбиты и смещается вдоль оси в положительном ее направлении. Анализируя второе уравнение системы (34), определим минимальное и максимальное расхождения спутников по высоте:

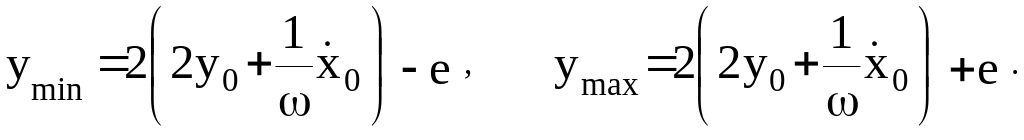
В предположении, что движение спутника происходит по круговой орбите радиуса , экстремальным расхождениям соответствуют минимальное и максимальное удаления спутника от центра масс центрального гравитирующего тела:

Таким образом, спутник будет обращаться по круговой орбите лишь при , т.е. при одновременном выполнении равенств:

В противном случае большая полуось орбиты спутника будет

Другими словами, размеры больших полуосей и орбит спутников будут различаться на величину

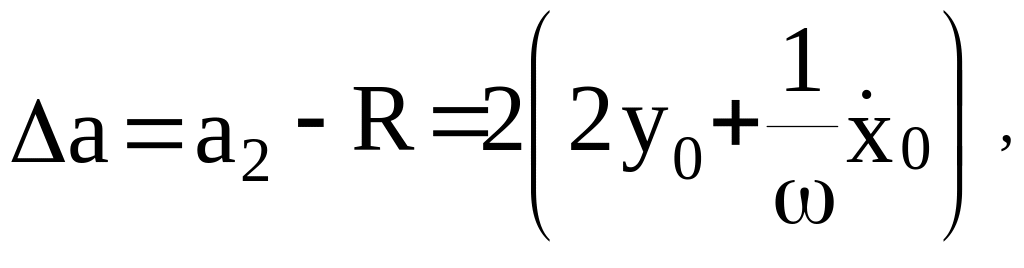
что в согласии с законом Кеплера приводит к различиям периодов их обращения на величину

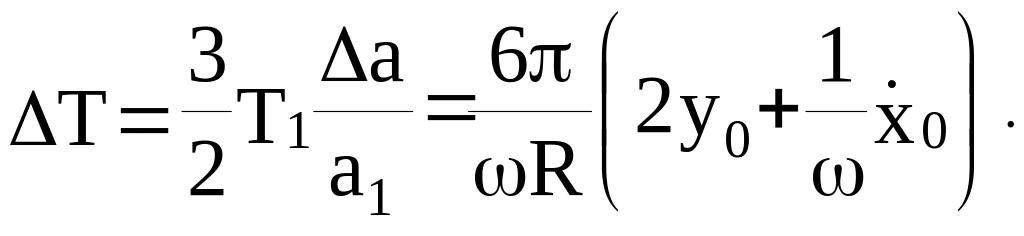
В общем случае в соответствии с (34) движение спутника относительно спутника происходит по сложному закону и представляет собой суммарное движение объекта по круговой орбите и по эллипсу. Такое движение содержит вековое расхождение спутников вдоль оси , обусловленное движением центра эллипса со скоростью (36).

Обратившись к третьему уравнению системы (32), проанализируем зависимость от начальных условий относительных боковых отклонений спутников. Сразу заметим, что текущее боковое отклонение определяется исключительно боковыми же начальными отклонениями в положении и в скорости . При , максимальное значение бокового отклонения будет равно и не будет зависеть от высоты орбиты. Напротив, при

откуда следует, что, чем выше орбита (т.е. чем больше период обращения спутника ), тем она чувствительней к начальным возмущениям боковой скорости .

До сих пор, говоря об относительном движении двух близких спутников, мы полагали, что орбита одного из них является круговой. Оказывается, полученные нами результаты описания относительного движения можно использовать и в случае, когда оба спутника обращаются по эллиптически орбитам. Для этого следует ввести опорное круговое движение третьего фиктивного спутника и связанную с ним орбитальную вращающуюся систему координат. Потребуем, чтобы отклонения координат и скоростей обоих реальных спутников от начала орбитальной системы координат были достаточно малы, обеспечивая возможность решения задачи в реальном приближении. Тогда для каждого реального спутника мы можем написать уравнение прогноза:

где 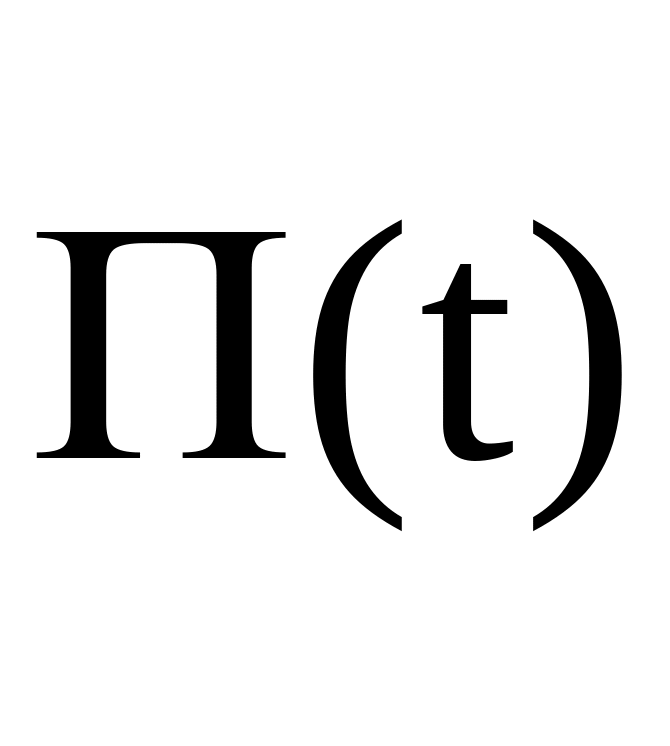– матрица прогноза, элементы которой суть функции интервала прогноза и угловой скорости опорного кругового движения фиктивного спутника. Образуем разность:

где и – вектора состояния движения спутника относительно спутника в начальный и конечный моменты времени, разделенные интервалом .