1) Выборочные средние

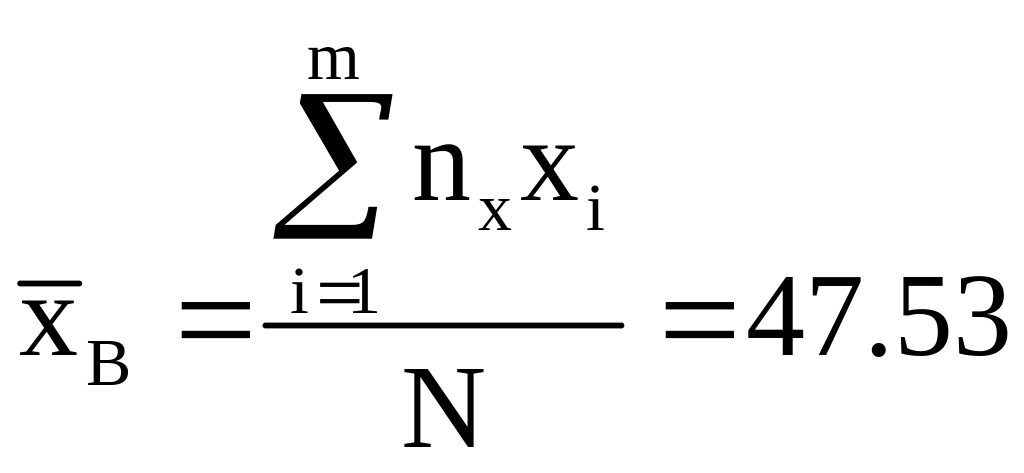
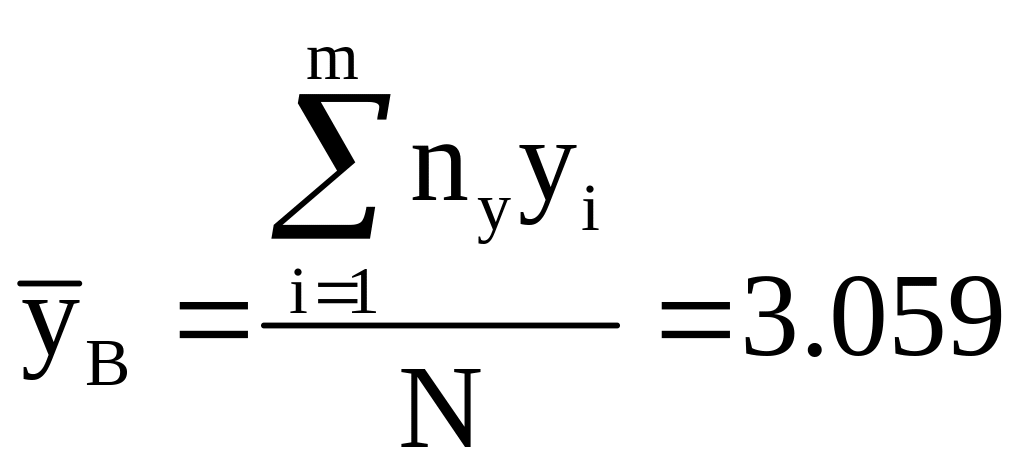
2 ) Квадрат стандарта.

Квадрат стандарта является несмещённой оценкой дисперсии , поэтому вместо среднеквадратического отклонения  будем подставлять в формулы корень из квадрата стандарта.

S_х = 10.96 S_y = 1.71

Подставим данные коэффициенты в формулу для вычисления выборочного коэффициента корреляции r_в

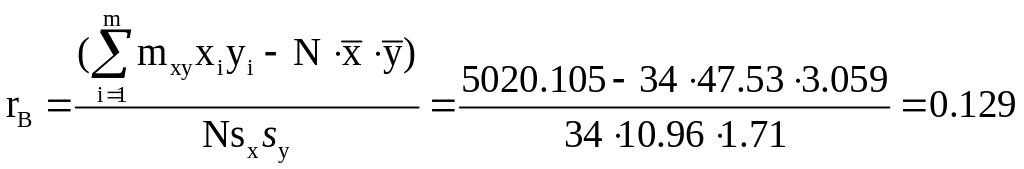
Теперь запишем уравнения теоретических линий регрессии

Y на X X на Y

Для построения прямых теоретических линий регрессий возмём пары

контрольных точек:

x = 20 x =50 y = 2 y = 4

y = 2.46 y = 3.06 x = 47.17 x = 48.82

Р ис 7.4

2. Проверка гипотезы о значимости коэффициента корреляции.

Пусть двумерная случайная величина (Х,Y) распределена по нормальному двумерному закону. Из генеральной совокупности извлечена выборка объёмом N образцов и по этой выборке вычислен выборочный коэффициент корреляции r_в.

При уровне значимости  требуется проверить нулевую гипотезу о том, что коэффициент корреляции r =0 при конкурирующей гипотезе о том, что r  0.

H₀ : r = 0

H_k : r  0

Если нулевая гипотеза отвергается, то это означает, что при заданном уровне значимости  выборочный коэффициент корреляции значимо отличается от нуля, а Х и Y коррелированы, т.е. связаны линейной зависимостью.

Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции не значим, а Х и Y некоррелированы, т.е. не связаны линейной зависимостью.

В качестве критерия проверки нулевой гипотезы примем случайную величину :

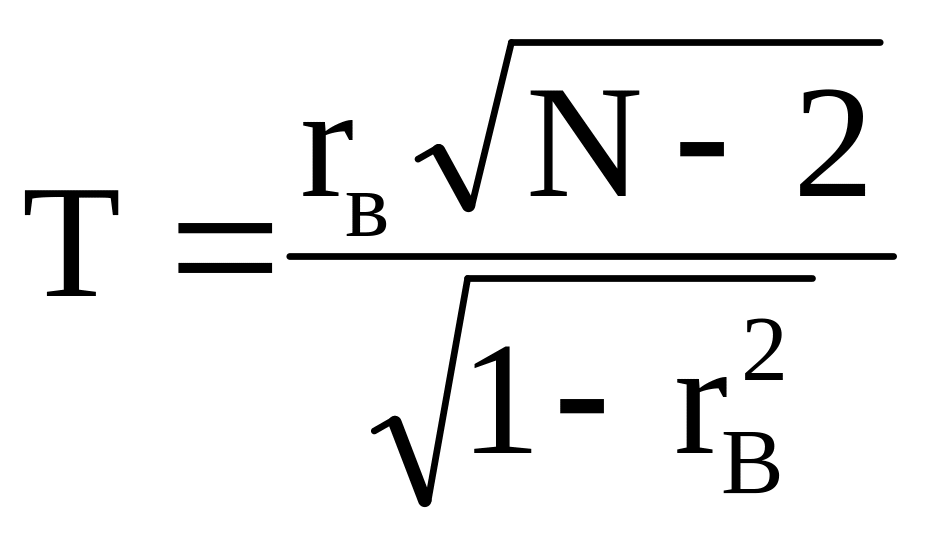(7.5)

Эта случайная величина распределена по закону Стьюдента с k = (N – 2) степенями свободы.

Поскольку конкурирующая гипотеза имеет вид r  0, критическая область – двусторонняя.

Для того, чтобы при заданном уровне значимости  проверить нулевую гипотезу Н₀: r = 0 о равенстве нулю коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе о том, что он не равен нулю H_k : r  0,надо вычислить наблюдаемое значение критерия:

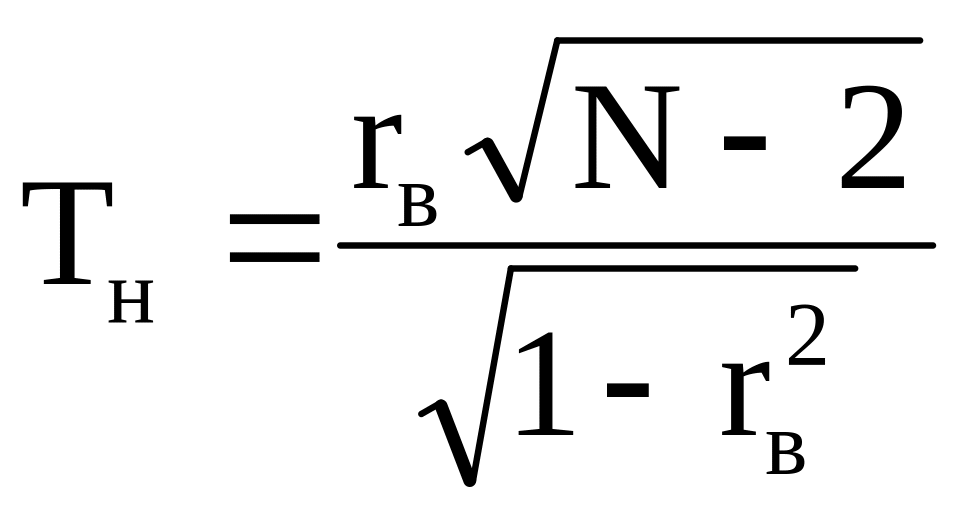(7.6)

Затем по таблице критических точек распределения Стьюдента, по заданному уровню значимости  и числу степеней свободы k = N – 2

в соответствии со стратегией Неймана-Пирсона найти критическую точку t_кр (,k).

Правило принятия решения будет следующим :

Если | Т_H |< t_кр – нет оснований отвергать нулевую гипотезу

Если | Т_H |> t_кр –нулевую гипотезу отвергают.

Если нулевая гипотеза отвергнута, значит отличие коэффициента корреляции r от нуля при заданном уровне значимости носит закономерный характер. Если же мы приняли нулевую гипотезу, следовательно отличие коэффициента корреляции r от нуля при заданном уровне значимости носит случайный характер.

Пример:

Вычислим значение Т_н : Т_н= 0.7359