Теория пластичности и ползучести Часть 3. Теории пластичности Содержание

1. Деформационная теория при одноосном растяжении

2. Деформационная теория при сложном нагружении

3. Пластическая деформация

4. Модель идеальной пластичности при одноосном растяжении

5. Ассоциированный закон пластического течения

6. Теория идеальной пластичности при сложном нагружении

7. Теория течения с изотропным упрочнением

8. Теория течения с трансляционным упрочнением

9. Обзор моделей пластичности в пакетах прикладных программ

10. Область применения моделей пластичности

1. Деформационная теория при одноосном растяжении

При одноосном нагружении тензоры напряжений и деформаций имеют вид:

, ,

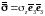где деформации, характеризующие сужение материала в направлениях, поперечных направлению нагружения, в силу изотропии материала равны друг другу . Такой вид нагружения удобен для наглядного представления закономерностей деформирования и нагружения, поскольку тензоры напряжений и деформаций при этом отображаются скалярам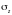и и (рис.1.1).

Рис.1.1

За недеформированное состояние примем ненагруженное, поэтому если , то и . Заметим, что устойчивость упругого материала требует, чтобы функция , изображенная на рис.1.1, была монотонно возрастающей, поэтому существует и обратная функция 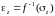, также монотонная. Модель материала, согласно которой точка состояния ( , ) в процессе нагружения и разгрузки скользит по одной и той же кривой

,

называется теорией малых упругопластических деформаций, или деформационной теорией. Добавим, что эта теория также представляет собой модель нелинейно упругого материала с диаграммой, снимаемой с образца при нагружении, без проверки того, как выглядит процесс разгрузки.

При неизотермическом нагружении упругого тела деформация однозначно зависит от напряжения и температуры T

.

Вспомним, что деформацию при нулевом напряжении называют тепловой . Температура, при которой , считается началом отсчета T₀ . Зависимость деформаций от напряжений удобнее записывать в виде суммы

, T = T – T₀ , (1.1)

разделяя деформацию на слагаемые: силовую деформацию и тепловую . При снятии напряжения силовая деформация упругого материала исчезает. Выражение (1.1) определяет линейно или нелинейно ведет себя упругое тело в случае неизотермического нагружения. Линейно упругое тело определяется выражением

.

Свойство упругости позволяет экспериментально определять тепловую деформацию , нагревая ненагруженные образцы. Зависимость тепловой деформации от температуры близка к линейной

,

где  – это коэффициент теплового расширения. Иногда это выражение уточняют следующим образом

,

где ₀ и _ – это константы материала: величина ₀ представляет значение производной при температуре начала отсчета T₀. Заметим, что в справочниках часто задают среднее значение  в том или ином температурном диапазоне, с тем или иным началом отсчета. Зависимость напряжений от деформаций имеет вид

,

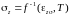где – это функция, обратная функции f по первому аргументу.

2. Деформационная теория при сложном нагружении

Из постулата симметрии следует, что при простом нагружении происходит и простое деформирование с тем же направляющим девиатором

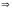
, . (2.1)

Поскольку любые траектории любых двух простых нагружений всегда подобны, то и траектории соответствующих деформаций в L₅ также подобны. Следовательно, зависимости при всех простых нагружениях (растяжение, сжатие, сдвиг, растяжение со сдвигом) с одинаковой историей или одинаковы. Эти соображения с учетом ряда других лежат в основе деформационной теории.

Для склерономного материала с оговоркой на монотонность нагружения, можно утверждать, что при простом нагружении зависимость одинакова и не зависит от направления направляющего девиатора. Если снять требование простоты нагружения и, таким образом, исключить из выражения (2.1) требование постоянства направляющих девиаторов, то получим деформационную теорию (теорию малых упругопластических деформаций), включающей в себя три основных соотношения:

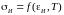, , . (2.2)

Здесь в первом соотношении постулируется линейная связь шаровых частей тензоров напряжений и деформаций, что подтверждается экспериментами. В третьем соотношении постулируется равенство направляющих девиаторов, наблюдаемое в изотропных средах, строго говоря, лишь при простых нагружениях. Второе соотношение является основным допущением, превращающим деформационную теорию в теорию нелинейной упругости, согласно которой свойства изотропных неупругих материалов, которые обнаруживаются при монотонном простом нагружении, абсолютизируются и предполагаются справедливыми при всех обстоятельствах. Все это позволяет получить весьма простую модель, сыгравшую, поэтому, важную роль в реологии.

Функцию, выражающую связь интенсивностей напряжений и деформаций при заданной температуре T

,

называют обобщенной диаграммой деформирования (единой кривой деформирования в интенсивностях). Для ее построения можно использовать аппроксимацию (2.9), где модуль упрочнения m₀ определяют из выражения (2.7). При пропорциональном нагружении изотропных материалов такая аппроксимация хорошо подтверждается экспериментами. Для удобства также можно использовать более простую зависимость (2.1).

Девиатор деформации представляет собой сумму двух слагаемых: упругого 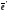и неупругого

.

С учетом этого выражения, а также принципа симметрии, следующего из постулата изотропии Ильюшина, траектория деформаций в девиаторном пространстве L₅ подобна не только траектории напряжений, но и траектории ее неупругой составляющей

,

что означает равенство направляющих девиаторов

и обусловливает связь соответствующих интенсивностей (рис.2.3б)

.

Требование устойчивости материала в деформационной теории сводится к ограничениям на значения упругих характеристик, наследуемым из теории упругости, и к требованию положительности производной функции . 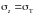Иногда диаграмма деформирования принимается в виде диаграммы идеально пластического материала (например, при одноосном растяжении участок упругого деформирования сменяется участком предельного состояния , на котором производная равна нулю). Это предельный случай границы между устойчивым и неустойчивым материалом, при котором возможно лишь кинематическое нагружение.

При деформировании пластичных материалов пластические деформации, как правило, существенно больше упругих, поэтому принимается, что при пластическом деформировании изменение объема пренебрежительно мало. На основании этого по­ложения вводится гипотеза о несжимаемости материала.