Точечные оценки мат. Ожидания и дисперсии. Состоятельность и несмещенность оценки (следовательно, исправленная дисперсия). Оценка вероятности события.
Точечная оценка применяется в тех случаях, когда:
- нам известен набор значений, которые принимает случайная величина Х
(набор получен в результате n независимых наблюдений)
-необходимо на основании этих значений оценить значение матожидания или дисперсии.
1. Матожидание.
У нас есть значения случайной величины Х, которые равны Х1, Х2, Х3… Х10. Это случайные величины, имеющие одинаковое распределение, совпадающее с распределением Х.
Можно составить выражение:
Х' = (Х1 + Х2 +Х3… +Х10)/10.
Х' – это выборочная оценка матожидания.
Закон распределения этой случайной величины Х' будет зависеть от закона распределения случайной величины Х, которое нам нужно найти.
Например, Х – это рост первого пассажира, который зашел в поезд метро. Х1, Х2, Х3 – конкретные значения, которые мы получили, когда измерили трех первых пассажиров. Х' – среднее арифметическое этих значений.
Так как законы распределения Х' и Х совпадают, их математические ожидания тоже совпадают. Ниже доказательство.
MX' = a = MХ.
В таком случае МХ’ – это оценка среднего роста пассажира, полученная с помощью оценки роста n (в данном случае 10) пассажиров.
Чем больше n, тем ближе оценка матожидания подойдет к реальному матожиданию.
2. Дисперсия.
Для оценки дисперсии служит формула:
или
S и D обозначают дисперсию (в «Математике для психологов» было обозначение S)
Деление на n дало бы заниженный показатель дисперсии, несмотря на то, что во втором множителе n членов. Деление на (n -1) дает более точный показатель.
Формула
является состоятельной, но не является несмещенной.
Дисперсию, полученную по первой формуле, называют исправленной дисперсией.
При больших значениях n значения дисперсии, полученные по первой и второй формуле, различаются мало.
Состоятельность и несмещенность – две характеристики рассмотренных оценок.
Состоятельность = при увеличении размера выборки оценка становится все более точной.
Несмещенность = по выборке любого размера оценка дает в среднем правильный результат (ее математическое ожидание равно оцениваемому параметру случайной величины).
Оценка вероятности события.
Пусть некоторое событие происходит с вероятностью Р, которая нам неизвестна. Однако мы можем произвести какое-то количество испытаний и посмотреть, сколько раз произойдет нужное нам событие.
Допустим, мы провели n испытаний, и событие произошло k раз.
Тогда точечная оценка Р' вероятности события Р будет равна n/k.
Р' = k/n.
Можно доказать несмещенность и состоятельность этой формулы.
При фиксированном значении n k является случайной величиной с биномиальным распределением. (см. ранее)
Тогда справедливы формулы:
Mk = nP; Dk = nP(1 – P).
(Для матожидания и дисперсии).
1. Докажем несмещенность оценки.
MP’ = M(k/n) = 1/n * Mk = 1/n * nP = P.
(В третьем шаге подставили формулу Мк = nP)
Таким образом, матожидание Р' = Р, что и утверждается в характеристике несмещенности.
2. Докажем состоятельность оценки.
(В 3 шаге подставили формулу Dk = nP(1 – P)).
В характеристике состоятельности утверждается, что при увеличении n увеличивается точность оценки.
При n = бесконечности дисперсия равна нулю, а значит оценка максимально точная.
На всякий случай: точечная оценка среднего квадратичного отклонения.
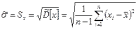
Доверительные интервалы. Построение доверительных интервалов для М.О. (при известных и неизвестных дисперсиях в параметрическом и непараметрическом случаях). Построение доверительных интервалов для дисперсии (при известном и неизвестном М.О.). Постановка вопроса и способ решения (использование уровней значимости, квантилей). –Задание 3.
Доверительный интервал — термин, используемый в математической статистике при интервальной оценке статистических параметров, более предпочтительной при небольшом объёме выборки, чем точечная. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Доверительные интервалы для мат. ожиданий
1)Неизвестная дисперсия
Р - вероятность
x̅ - выборочное среднее
S - выборочное среднеквадратичное
γ - уровень надёжности
α - уровень значимости
n - объём выборки
Доверительный интервал:
Р {x̅-ε < a < x̅+ε} = γ = 1-α
Р {|x̅-а| < ε} = γ = 1-α
α
- задан; ε – найти
— случайная величина из распределения Стьюдента
Р {|t| < tα} = γ = 1-α ***
***=> P {t > tα} = α/2 (P {t < -tα} = α/2)
Алгоритм нахождения доверительного интервала:
При заданном α находим двусторонний квантиль tα (в таблице Стьюдента берём α/2)
aα- = x̅-ε; aα+ = x̅+ε
Далее пример таблицы, при n=17, x̅=170, s=11
2)Известная дисперсия
σ - стандартное отклонение
N - нормальное распределение случайной величины
l - случайный интервал
σ=s
X ~ N (a;σ)
С
лучайная
величина x̅ ~ N (a; σ/ √n)
Доверительный интервал:
Р {|x̅-а| < ε} = 1-α = γ
[
1]:
— стандартное нормальное распределение
[
1]=
Алгоритм:
Известно α => γ/2 => по таблице Ф0 или Ф(А3) получаем Хα'
aα- = x̅-ε; aα+ = x̅+ε
П
ример
таблицы:
Доверительные интервалы для среднеквадратичного отклонения
1)Неизвестно мат ожидание
МХ = а
Доверительный интервал:
Хиα+; Хиα- - верхние и нижние двусторонние квантиль для распределения Хи-квадрат (с n-1 степени свободы)
Алгоритм:
α=> α/2; 1- α/2
Хиα+; Хиα-
σα-; σα+
Пример таблицы:
2)Известно мат ожидание
МХ=а
Доверительный интервал:
П
ример
таблицы:
Непараметрическая модель доверительных интервалов
Точная оценка для мат ожиданий (непараметрическая модель)
(х1, ... ,хn) n
вариационный ряд
точечная оценка
â
= med {Σ', ... ,Σ^N} =
Знаково-ранговые статистики Вилкоксона
(
про
это уже писали, поэтому кину просто из
лекции Александровой)
*
**
Знаково-ранговые характеристики Вилкоксона
Если немного покопаться на сайте stat-msu, то буквально в следующей теме можно было найти полное решение таблицы из ДЗ (для ленивых - рис.3). Собственно, ее и задали нам посчитать, но дабы не сесть в лужу, поговорим о каждом пункте подробнее.
1. Первые три строчки нам даны изначально, думаю, смысла о них говорить нет.
2. z=y-x - это все, что вам необходимо знать о z, и чего не было написано в таблице на доске в классе, но записано на картинке.
3. |z| - это модуль. Просто отбрасываем от предыдущего нашего значения z минус и радуемся.
4. R(|z|) - это ранг. Он считается просто: нужно выписать в порядке возрастания все значения того, что в скобках (в нашем случае это |z|), пронумеровать их и именно этот номер вписать в табличку. Все.
5. z+ и z- по аналогии рис.1: z+ = 0, если z<0 и т.п.
6. Этого в таблице нет, но задано еще посчитать некие W+ и W-. Формула - рис.2 т.е. это ничто иное как просто сумма всех z+ и z- соответственно.
Это разбор третьего задания из группы Ken sy my nommer?
Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Рассмотрим вероятностное пространство и — вероятностная мера, задающая распределение некоторой случайной величины