17. Магнитное поле. Вектор магнитной индукции. Закон Био-Савара

Магнитное поле - это особый вид материи, невидимый и неосязаемый для человека, существующий независимо от нашего сознания.  Еще в древности ученые-мыслители догадывались, что вокруг магнита что-то существует

Вектор  магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой маг­нитного поля является вектор магнитной индукции.

Магнитная индукция  В зависит от I и r, где r — расстояние от проводника с током  до исследуемой точки. Если расстояние от проводника много меньше его длины (т. е. рассматривать модель бесконечно длинного проводника), то ,

где k — коэффициент пропорциональности. Подставляя эту формулу в уравнение для силы взаимодействия двух проводников с током, получим F=B ^.I^.ℓ.

Отсюда   .

Таким образом, модуль вектора магнитной индукции  есть отношение максималь­ной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка.

Единица измерения в СИ - тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла.

Закон Био Савара Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке.

  Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.

Формула 1 — Закон Био Савара Лапласа

 где I     ток в контуре

     гамма контур, по которому идет интегрирование

     r0    произвольная точка

18. Расчет магнитных полей с помощью закона Био-Савара. Магнитное поле кольцевого и прямого таков.

Закон Био-Савара-Лапласа: вектор индукции магнитного поля, созданного элементом проводника  , по которому течет ток  , имеет вид:

 

  ,                                      (1)

где  – радиус-вектор, проведенный от элемента   до той точки, в которой определяется индукция поля;   – магнитная постоянная.

·     В скалярной форме

,                                             (2)

где  – угол между векторами   и  .

·     Индукция магнитного поля в произвольной точке А, созданного отрезком проводника с током  конечной длины,

,                                (3)

где   – расстояние от т. А до проводника;   – углы, образованные радиус-вектором, проведенном в т.А соответственно из начала и конца проводника, с направлением тока.

В качестве постоянной интегрирования выберем угол α. Из рис. выше имеем 

Подставив эти значения в формулу

, получим

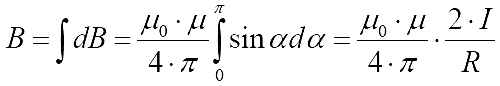
Таким образом, для бесконечно длинного прямолинейного проводника с током:

Для магнитного поля тороида (кольцевой катушки с витками, намотанными на сердечник, имеющей форму тора, по которой течёт ток).

 

Магнитное поле отсутствует вне тороида, а внутри его оно является однородным (рис. ниже).

Линии магнитной индукции, как следует из соображений симметрии, есть окружности, центры которых расположены на оси тороида.

Используя теорему о циркуляции вектора B (будет рассмотрена позже) можно показать, что

где N – число витков тороида.