ЛАБ2 - Исследование позиционных динамических звеньев

МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И. НОСОВА»

Кафедра автоматизированного электропривода и мехатроники

Лабораторная работа № 2

Исследование позиционных динамических звеньев

Выполнил:

Проверил:

Магнитогорск, 2019

Исследование позиционных динамических звеньев

Цель работы: Математическое моделирование временных характеристик позиционных звеньев. Изучение динамических свойств, частотных характеристик и оценка влияния параметров на свойства звеньев. Ознакомление с системами MATLAB и MathCAD. Применение этих систем для изучения динамических звеньев.

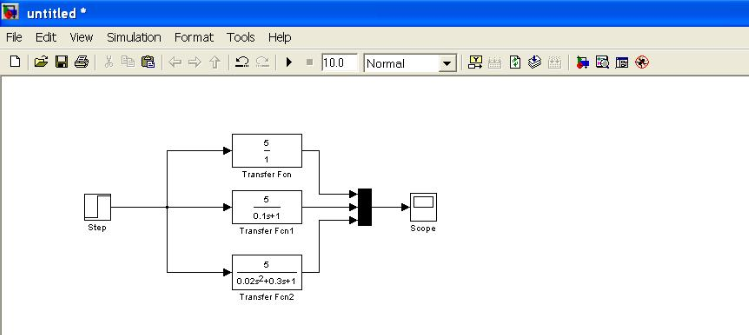
Рисунок 1 – Схема модели для исследования пропорционального

и апериодических звеньев.

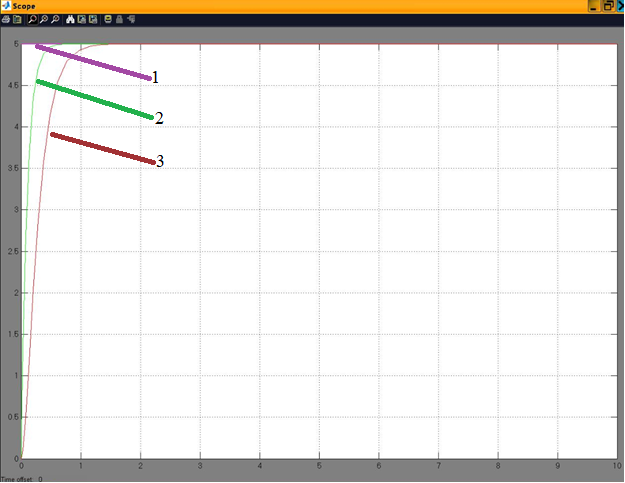
Рисунок 2 – Графики переходных функций полученных со Scope: 1 – пропорциональное звено; 2 – апериодическое звено первого порядка; 3 – апериодическое звено второго порядка.

Рисунок 3 – Графики переходных функций полученных с LTI VIEWER: 1 – пропорциональное звено; 2 – апериодическое звено первого порядка; 3 – апериодическое звено второго порядка.

Рисунок 4 – Графики импульсно-переходных функций полученных с LTI VIEWER: 1 – пропорциональное звено; 2 – апериодическое звено первого порядка; 3 – апериодическое звено второго порядка.

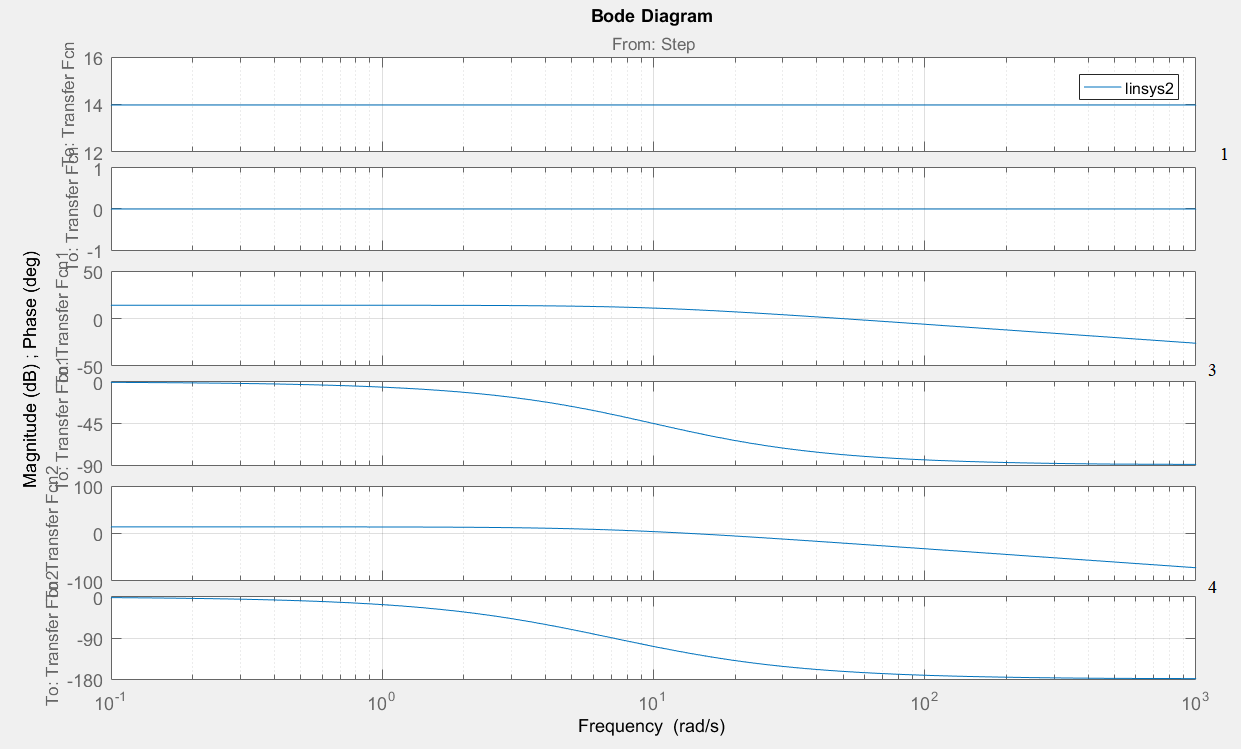
Рисунок 5 – Логарифмические частотные характеристики: 1 – пропорционального звена; 2 – апериодическое звено первого порядка; 3 – апериодическое звено второго порядка.

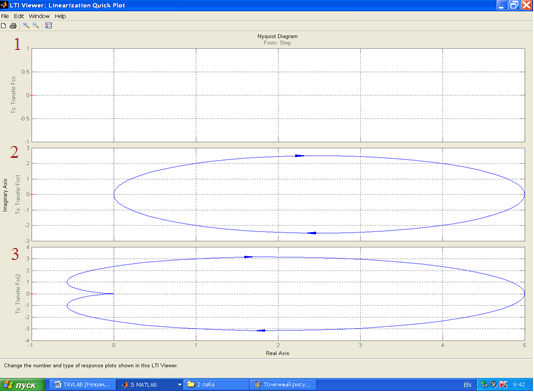
Рисунок 6 – Комплексно–частотные функции: 1 – пропорционального звена; 2 – апериодическое звено первого порядка; 3 – апериодическое звено второго порядка.

Исследование переходной функции h(t) колебательного звена

Рисунок 7 – Схема модели для исследования переходной функции

колебательного звена.

Рисунок 8 – График переходной функции колебательного звена полученный со Scope.

Рисунок 9 – График переходной функции колебательного звена полученный с LTI VIEWER.

Рисунок 10 – График импульсно-переходной функции колебательного звена полученный с LTI VIEWER.

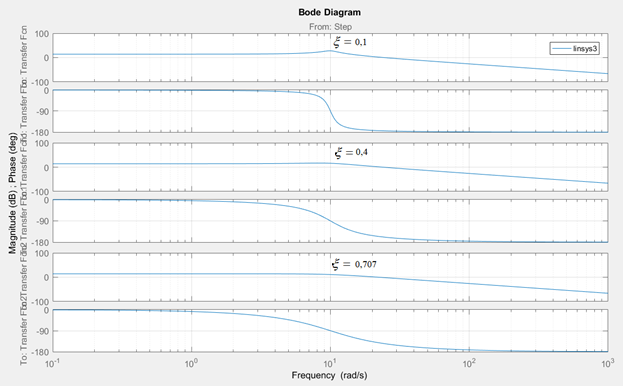
Рисунок 11 – Логарифмические частотные характеристики колебательного звена.

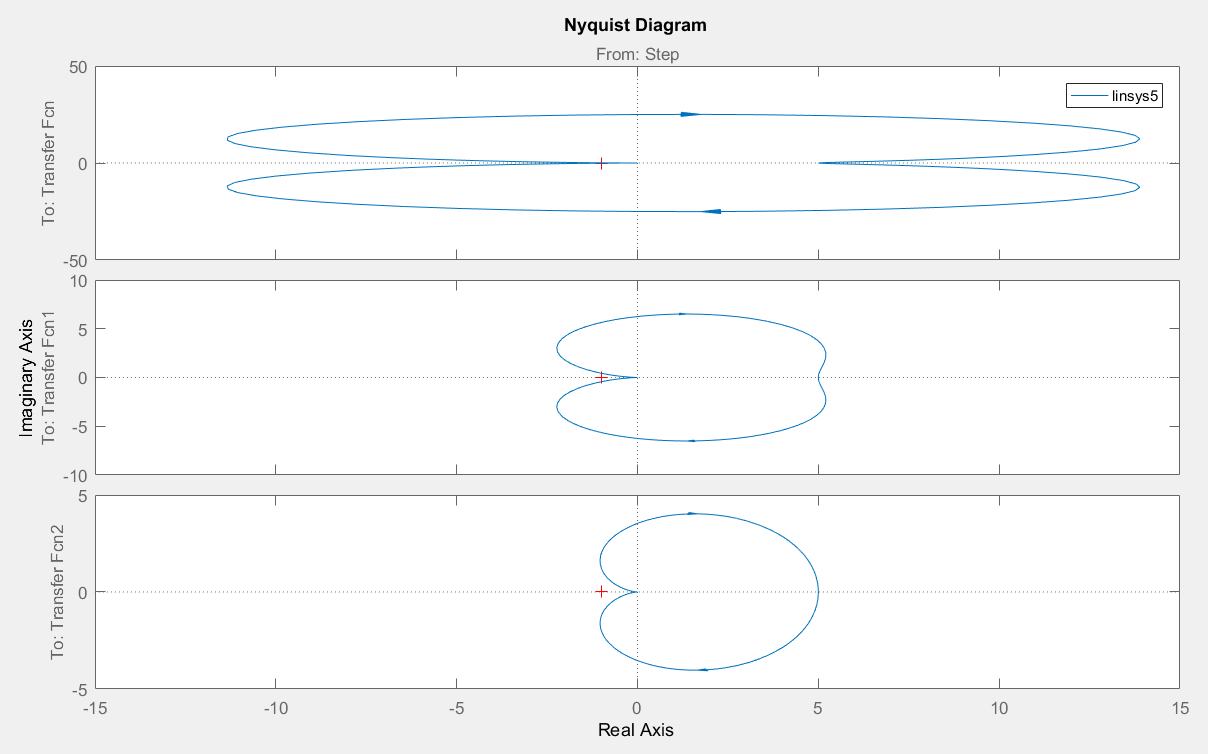
Рисунок 12 – Комплексно–частотные функции колебательного звена.

Исследование переходной функции h(t) консервативного звена

Рисунок 13 – Схема модели для исследования переходной функции

консервативного звена.

Рисунок 14 – График переходной функции консервативного звена полученный со Scope.

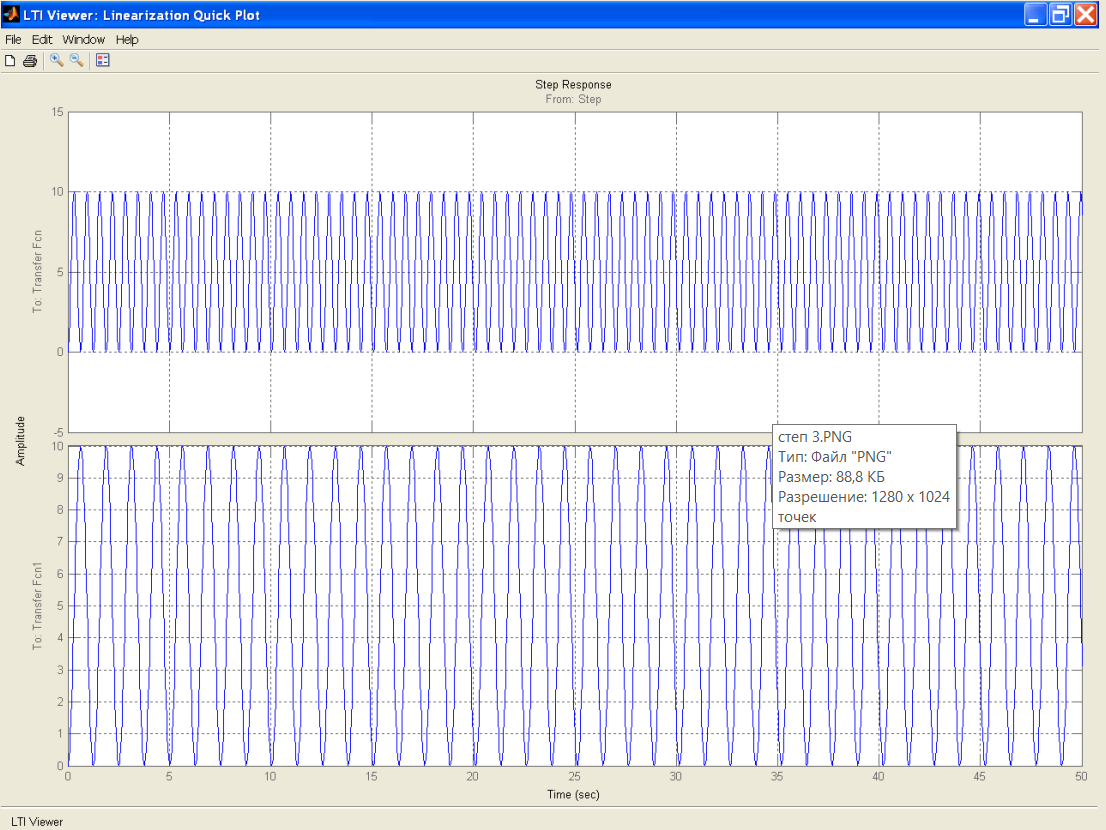
Рисунок 15 – График переходной функции колебательного звена полученный с LTI VIEWER.

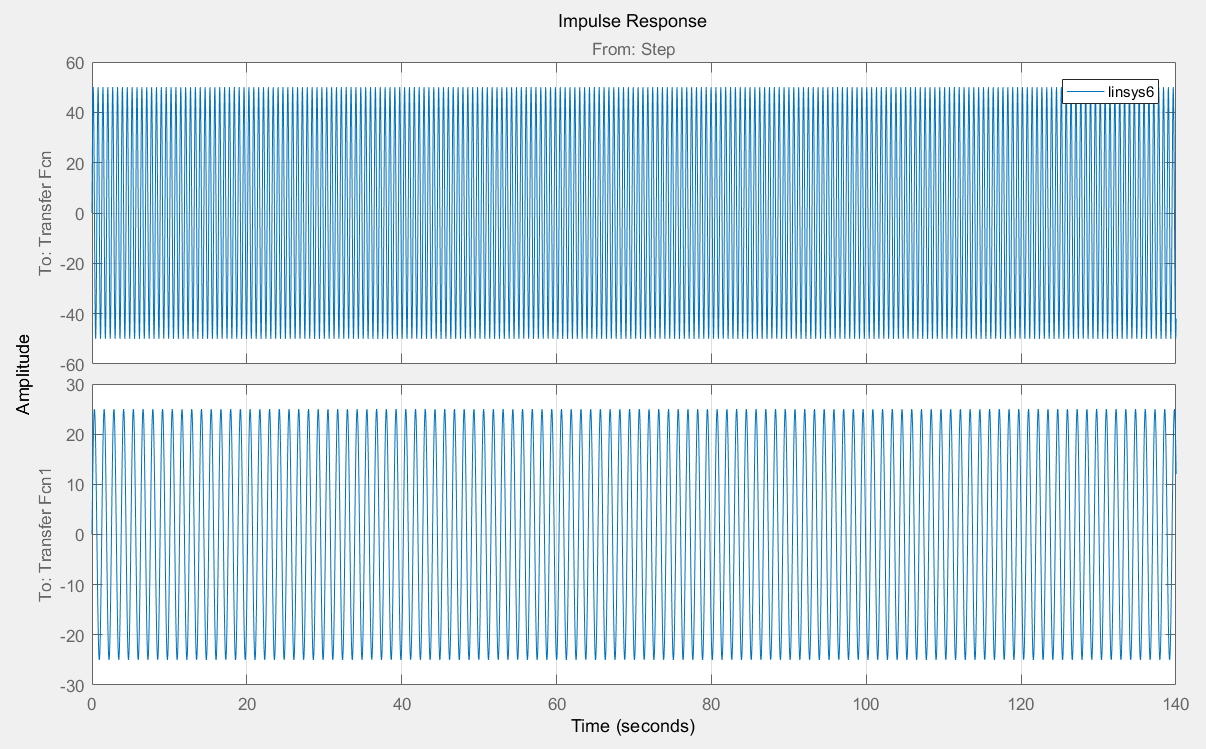
Рисунок 16 – График импульсно-переходной функции консервативного звена полученный с LTI VIEWER.

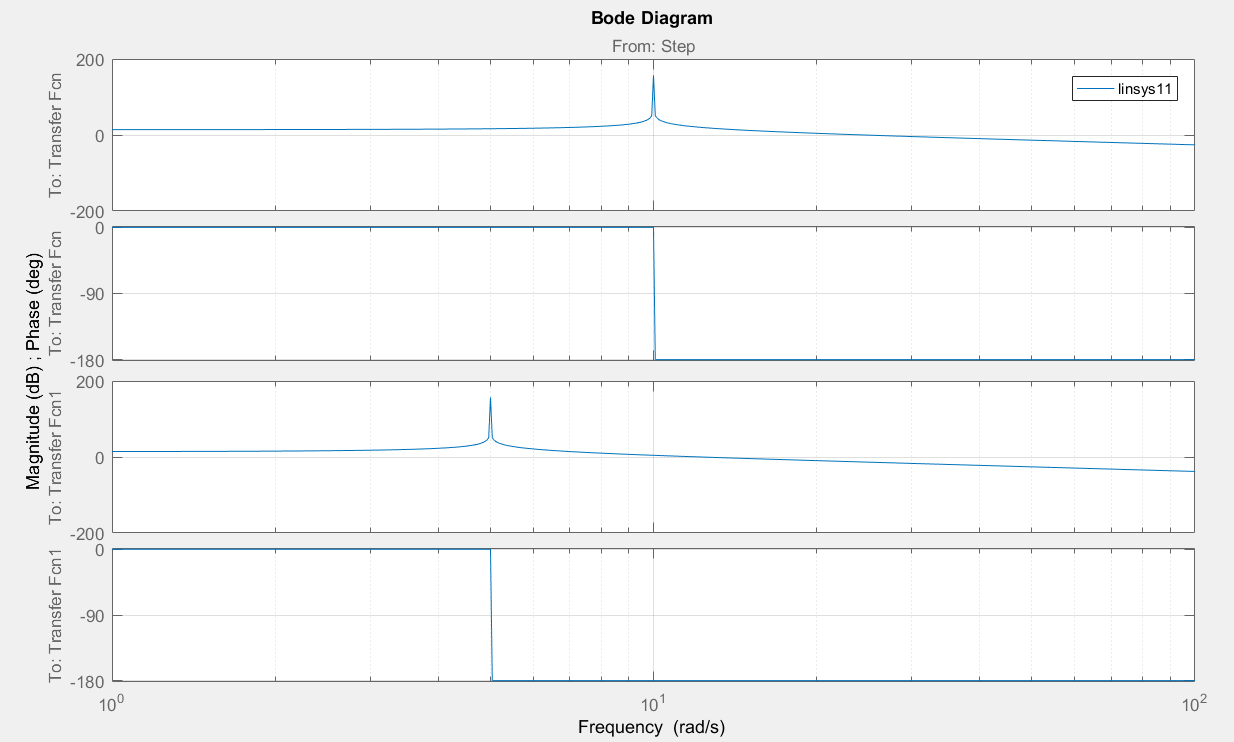
Рисунок 17– Логарифмические частотные характеристики консервативного звена.

Рисунок 18 – Комплексно–частотные функции консервативного звена.

Вывод: в ходе данной лабораторной работы были изучены временные характеристики типовых динамических звеньев с использованием автоматизированных средств моделирования на ПК Matlab, Simulink, также были построены реакции каждого типового звена с заданными параметрами на ступенчатое и импульсное входное воздействие и определены как влияют коэффициенты, входящие в описание каждого звена, на параметры переходного процесса