6. Функциясы бойынша 252 мен 468 діңЕкое ін табу керек.

EKOE(468,252)= =

468*7=3276

EҮOБ(468,252)=36

6-билет.

1.Қалындылар класының сақинасы.

Барлық бүтін сандар жиынын r модулы бойынша, мынадай принципке сүйене отырып, сандар класына бөлеміз: r санына бөлгенде бірдей қалдаық шығатын барлық бүтін сандарды класқа жатқызамыз.

Айталық ( modr) бойынша барлық кластар k₀, k₁, …k_r-1болсын. Әрбір класс сол кластың кез келген өкәлә арқылы бір мәнді анықталады. Әрбір кластан бір-бір өкіл белгілеп алайық: p₀, p₁, p₂,… p_r-1, p_i k_i(i=0,1,2 …r-1). Сандар кластарын өзара қосуға, азайтуға және көбейтуге болады.

Яғни, ( modr) бойынша кластың қосындысы, айырмасы және көбейтіндісі де ( modr) бойынша класс болып табылады.

Сонымен, ( modr) бойынша барлық кластардың жиыны сақина құрайды, мұндай сақина ( modr) қалындылар кластарының сақинасы деп аталады.

Мысал. Айталық r =6 болсын. ( mod6) бойынша барлығы 6 класс бар: k₀, k₁, k₂, k₃, k₄, k₅. Бұл кластардың өкілдері сәйкес мыналар: 0, 1, 2, 3, 4, 5.

Мыналардың орындалатынын байқау оңай:

k₂+ k₅= k₁k₃+k₂= k₅k₀+ +k₃= k₃

k₅- k₃= k₂k₁-k₄= k₃k₂- -k₀=k₂

k₃ k₄= k₀k₂ k₅= k₄k₃ k₅=k₃т.с.с.

Кез келген класы үшін болады.Кластарды қосу амалы орын ауыстырымдылық заңына бағынады:

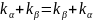
және де терімділік (ассоциативтік) заңына бағынады:

Сондай-ақ кластарды көбейту амалы коммутативтік заңына бағынады:

және де терімділік заңына бағынады:

Сонымен, ( modr) қалындылар кластарының сақинасы әрі коммутативтік, әрі ассоциативтік сақина болып табылады да, оған енетін элемент (класс) саны шектеулі болады. ( modr) кластардан группалар құрауға болады.

2. Мебиус функциясы, қасиеттері.

Бір жағдайда аргументтің өзгеру облысы тек қана бүтін сандар да, екінші бір жағдайда нақты сандар болуы мүмкін. Сондықтан да бұл ф/ялар сандық ф/ялар деп аталады. Мебиус ф/ясы сандық ф/я болып табылады. Оны деп белгілейді. Мебиус ф/ясы аргументінің тек қана бүтін оң мәндерінде анықталған, атп айтқанда: