№4 Емтихан билеті

1-сұрақ: Z тегі салыстырудың негізгі қасиеттері.

1-қасиет (рефлексивтік қасиеті): Кез келген сан өзімен өзі салыстырымды:

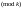
Шынында да, айырмасы қашан да 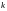санына бөлінеді.

2-қасиет (симметриялық қасиеті): Егер болса, онда болады.

Шынында да, мен айырмалары санына бірдей бөлінеді.

3-қасиет (транзитивтік қасиеті): Егер және болса, онда болады. Шарт бойынша қосындысы да ға бөлінеді, яғни .

4-қасиет. Салыстырудың кез келген мүшесін бір жағынан екінші жағына кері таңбамен көшіруге болады. Шынында да, айталық делік, сонда айырмасы ға бөлінеді, олай болса 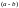айырмасы модулі бойынша 0 санымен салыстырымды . Дәл осылай немесе

5-қасиет. Модульдары бірдей екі не бірнеше салыстыруларды мүшелеп қосуға не азайтуға болады. Айталық мына салыстырулар берілген болсын: және . Сонда , айырмалары, демек, олардың қосындысы.

және айырмасы де ға бөлінеді, сондықтан 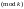немесе . Егер салыстырулар берілген болса, , , …., онда да дәл былай жазуға болады: Дербес жағдайда, егер .

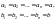
Салдары: Салыстырудың екі жақ бөлігін де бірдей бүтін санға көбейтуге болады.

6-қасиет: Модульдары бірдей екі не бірнеше салыстыруларды мүшелеп көбейтуге болады. мен айырмалары ға бөлінеді, олай болса, олардың көбейтіндісі 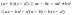де ға бөлінеді. Бұл теңдіктен айырмасының ға бөлінетіндігі шығады, яғни .

Салдары: Егер болса, онда кез келген натурал сан болғанда, болады. Басқаша айтқанда, салыстырудың екі жақ бөлігін де бірдей дәрежеге шығаруға болады.

7-қасиет: Салыстырудың екі жақ бөлігін де модульмен өзара жай сан болып табылатын олардың ортақ бөлігіне бөлуге болады. Айталық және 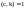делік, сонда өзара жай сандар жөніндегі негізгі теорема. яғни

8-қасиет: Салыстырудың екі жақ бөлігін де және модульды бұлардың ортақ бөліміне бөлуге болады. болсын, мұнда сандарының ортақ бөлгіші. Ал саны яғни

9-қасиет: Бірнеше модуль бойынша өзара салыстырымды сандар осы модульдардың ең кіші еселігіне тең модуль бойынша да салыстырмалы болады. 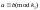, ,…, мұнда . Егер және ның кез келген бөлгіші болса, онда да 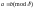болады.

10-қасиет: Егер бүтін 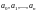коэффициентті полином болса және де егер бүтін r мен s үшін болса, онда болады. 6 қасиет бойынша , , … , .

2- сұрақ: теңдігін және лайықты бөлшектердің қысқармайтындығын дәлелдеу.

Егерде мен 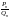кез келген тетелес тұрған екі лайықты бөлшек болса, онда немесе қатысы орынды. Шынында да, мен лайықты бөлшектері үшін (1) қатыстың орынды екендігін тікелей тексеру тексеру арқылы байқаймыз:

Айталық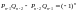 (2) . Онда 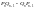-ге

қатыстан мен нің мәнін тауып алып қойсақ: немесе (2)-ге сүйенсек: екенін табамыз. Дәлелдеу керегі де осы еді. (1) қатыстың біріншісі екіншісін -ге бөлуден шығады. Лайықты бөлшектер-қысқармайтын бөлшектер. Шынында, айталық 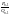мен үздіксіз бөлшектің көршілес екі лайықты бөлшектері болсын. Онда . Бұл қатыстан лайықты бөлшегінің алымы мен бөлімі -нің 1-ден басқа ортақ бөлшігі жоқ екендігі көрініп тұр.

3-сұрақ: Векторлық кеңістіктегі векторлардың скаляр көбейтіндісі. Ортогональ векторлар системасы.

Векторлық кеңістік деп кез келген сызықтық комбинациясы осы кеңістікте жататын векторлар жиынын айтады. Анықтама: мен векторларының скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың бұрышының косинусының көбейтіндісіне тең немесе , санын айтады.

, . Скаляр көбейтіндінің келесі қасиеттері бар

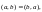
Анықтама: эвклид кеңістігінің x,y векторы ортогональды болады деп аталады. Егер олардың скаляр көбейтіндісі (х, у)=0 болса.

4-сұрақ: Алгебралардың гомоморфизмдері мен изоморфизмдері

екі мультипликативті группа берілген. Анықтама G группа H группаға гомоморфизм болады. H бейнелеу. Ол G жиынын H жиынға бейнелейді. Бұл бейнелеу де G ның басты операциялары сақталады. Яғни 1) , 2)

Мысалдары:

1) 0 ден өзгеше барлық рационал сандар жиыны

рационал сандардың мультипликативті группасы

оң рационал сандардың мультипликативті группасы

ны ға бейнелейтін үшін басты операциялары сақталады. ның абсолют шамасы һ бейнелеу гомоморфизм болады.

Дәл/уі: 1) , , , , 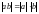; 2) ,

Кэли теоремасы: группа G жиынындағы симметриялық группаға болады. Осындай теорема жарты группа үшін де айтылады. Кез келген бірлік элементтермен бірге жарты группа G жиынындағы симметриялық жартылай группаға изоморфты болады.

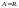
5-сұрақ: қатынасын рефлексивті, симметриялы, антисимметриялы және транзитивтілік қасиеттерін зерттеу керек.

1)симметриялы емес, себебі мысал:

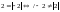
2)антисимметриялы, себебі мысал:

3)рефлексивті емес, себебі мысал:

4)транзитивті емес, себебі , мысал:

6-сұрақ: 299, 391 және 667 сандарының ЕҮОБ ін табу керек.

ЕҮОБ (299, 391, 667) = 23

16-билет

1.Вильсон теоремасы

Кез-келген жай р саны үшін мына салыстыру (р-1)! + 1 0(mod p) орындалады.

Вильсон теоремасының тамаша қасиеті – оның қайтарымдылығы, атап айтқанда: егер р саны үшін мына салыстыру (р-1)! + 1 0(mod p )Орындалатын болса, онда р- міндетті түрде жай сан болады. Шынында да, айталық р-құрама сан, ал δ - оынң 1-ден өзгеше бөлгіштерінің бірі делік. Сонда мына салыстырудан (р-1)! -1 (mod p) не мына теңдіктен (р-1)! -1+ ps шығатыны: (-1) саны да δ- ға бөлінеді. Бұлай болуы мүмкін емес. Осы табылған қарама-қайшылық біздің ұйғаруымызды дәлелдеп береді. Сонымен, мынадай қорытынды жасаймыз: Р жай сан болуы үшін оның (р-1)! + 1 0(mod p) салыстыруын қанағаттандыруы қажетті және жеткілікті. Сонымен, Вильсон теоремасы жай сандардың структуралық құрылысын сипаттайды.

2. Симметриялы көпмүще туралы лемма.

Виет теоремасы

x₁+x₂+x₃=σ₁

x₁ x₂+x₂ x₃+ x₁x₃=σ₂

x₁+x_{2+ ,,,} x_{n +}

x₁ x₂+ x₁x_{3+ ,,,,+} x₁x_n+ x₂ x₃++ x₂ x₄+,,,+ x_n-1 x_n= σ₂

x₁ x₂x₃+ x₁ x₂ x_4+,,,= σ₃

x²+px+q=0

x₁+x₂= -p= σ₁

x₁ x₂ = q= σ₂

(x-x₁)(x₁-x₂)(x₂-x₃)= 0

x³+px²+qx+r=0

x1+x2+x3=σ1=-p

x₁ x₂+x₂ x₃+ x₁x₃=σ₂=q

x₁ x₂x₃=- σ₃= r

3.Әртүрлі базистегі вектор координаталарының байланысы.

Қандай да бір е базисінің координаталары берілсін. {e} = {e₁,e₂, e₃}Dim e=3, яғни е базисі 3 өлшемді.Тура осылай базисінің координаталары берілсін{e} = { , }

{e}: x= (x₁,x₂,x₃)

: x’= ( , )

e₁= (a₁₁, a₁₂, a₁₃)

e₂₌ (a₂₁, a₂₂, a₂₃)

e₃= (a₃₁, a₃₂, a₃₃)

=( )

=( )

=( )

X=A = A

= ₊ a₁₂₊

= ₊ a₂₂₊

= ₊ a₃₂₊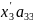

4. Сақина ұғымы, сақинаның қарапайым қасиеттері.

Сақина — қазіргі алгебраның негізгі түсініктерінің бірі. Сақина деп бос емес R жиынын айтады. Осы жиынның белгілі бір ретпен алынған кез келген а, b және с элементтері үшін: 1) a+b= =b+a қосудың коммутативтілік; 2) a+(b+c)=(a+b)+c қосудың ассоциативтілік; 3) a+x=b теңдеуінің x=b-a шешуі болатын қосудың c дистрибутивтілік шарттарынb+a(b+c)=aқайтымдылық; 4) a қанағаттандыратын қосу және көбейту амалдары анықталады. Сақина алгебрадан басқа функционалдық талдауды жетілдіруде операторлар сақинасы, функция сақинасы түрінде қолданылады.

Сақинаның қарапайым қасиеттері.

Теорема. (Р, +, ) сақинасы үшін мына қасиеттер орындалады: a, b, c P

элементтері үшін

1⁰. 0 элемент біреу ғана;

2⁰.

3⁰. a + b = a b = 0

4⁰. a + b = 0 b = a

5⁰. a + x = b x = b - a

6⁰. а) a + b = a + c b = c

б) a + c = b + c a = b

7⁰. 0 a = a 0 = 0

8⁰. (-a)b = a(-b) = -(ab)

9⁰. (-a)(-b) = ab

10⁰. (a – b)c = ac - bc

11⁰. a(b – c) = ab - ac

Дәлелдеуі. 1⁰ - 6⁰ қасиеттер топтың қасиеттерінен белгілі.

7⁰. 0 a = (0 + 0)a = 0 a + 0 a 0 a = 0

Осымен бірдей a 0= 0 дәлелденеді.

8⁰. ab + (-a)b = (a + (-a))b = 0 (-a)b = -(ab)

Осымен бірдей дәлелденеді.

9⁰. (-a)(-b) = (8⁰) = -(a(-b)) = -(-(-ab)) = (2⁰) = (ab)

10⁰. (a – b)c =(a + (-b))c = ac + (-b) c = ac + (-(bc)) = ac -bc

Осымен бірдей 11⁰ дәлелденеді.

Ішкі сақина. (P, +, ) сақина берілген болсын. L P.

(L, +, ) алгебралық жүйесі сақина болатын болса, онда оны (P, +, ) сақинаның ішкі сақинасы деп атайды.Мысалы, 2Z - жұп сандар жиыны. 2Z Z.

(2Z, +, ) сақина болады және ол (Z, +, ) сақинасының ішкі сақинасы болып табылады.

Анықтама. Нөлден басқа барлық элементтерінің керісі болатын коммутативті сақинаны өріс деп атайды. Өрісті (F, +, ) деп белгілейміз. Олай болса өрісті сақинаның аксиомаларына қосса

1) ab = ba, a, b, F

2) a, F, ⱻ a^-1 F : aa^-1 = 1

Сонымен, (F, +, ) алгебрасы өріс болса, онда (F, +) және (F, ) екеуі де абельдік топ болады. Оларды сәйкес өрістің аддитивті және мультипликативті топтары деп атайды.