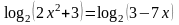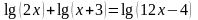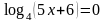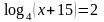Практическая работа №3
Тема: Нахождение значений логарифма по произвольному основанию. Переход от одного основания к другому. Решение логарифмических уравнений.
Цель: Закрепить навыки выполнения арифметических действий выражений, содержащих логарифмы, и навыки решения логарифмических уравнений.
Ход работы:
Теория (ответить на контрольные вопросы и привести примеры)
Контрольные вопросы:
Дать определение логарифма, десятичного логарифма.
Записать свойства логарифмов.
Практика
1. Вычислить:
1 вариант |
2 вариант |
||
|
|
|
|
2. Решить уравнения:
№ |
1 вариант |
2 вариант |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Практическая работа №4
Тема: Взаимное расположение прямых, прямых и плоскостей, плоскостей. Геометрическое преобразование пространства.
Цель: Закрепить знания по темам «Взаимное расположение прямых, прямых и плоскостей, плоскостей» и «Геометрическое преобразование пространства».
Развивать пространственное воображение и логическое мышление.
Ход работы:
Теория (ответить на контрольные вопросы устно)
Контрольные вопросы:
Основные понятия стереометрии.
Определения отрезка, луча, угла, вектора.
Определения параллелограмма, прямоугольника, квадрата, ромба, трапеции.
Аксиомы стереометрии.
Следствия из аксиом стереометрии.
Взаимное расположение прямых в пространстве.
Взаимное расположение прямой и плоскости.
Взаимное расположение плоскостей.
Признак параллельности прямых.
Признак параллельности прямой и плоскости.
Перпендикулярные прямые в пространстве.
Признак перпендикулярности прямой и плоскости.
Свойства перпендикулярности прямой и плоскости.
Признак перпендикулярности плоскостей.
Примеры движения.
Гомотетия
Практика
Начертить четырехугольник и построить ему симметричный относительно оси.
Начертить треугольник и построить ему симметричный относительно центра.
Начертить четырехугольник и выполнить его параллельный перенос.
Построить треугольник гомотетичный данному, если коэффициент гомотетии равен 2
Изобразить на плоскости куб, параллелепипед, треугольную призму, пирамиду, усеченную пирамиду.
Практическая работа №5
Тема: Задачи на подсчет числа размещений, перестановок и сочетаний. Вывод бинома Ньютона n степени.
Цель: Закрепить навыки использования формул комбинаторики и действий с факториалами. Научиться выводить бином Ньютона любой степени и использовать треугольник Паскаля
Ход работы:
Теория (ответьте на контрольные вопросы, приведите примеры).
Контрольные вопросы:
Что такое факториал?
Запишите формулы числа перестановок, сочетаний, размещений.
Приведите примеры комбинаторных задач на каждую из формул.
Что такое бинома Ньютона?
Запишите свойства биномиальных коэффициентов.
Что такое треугольник Паскаля?
Практика
№ |
1 вариант |
2 вариант |
1 |
Вычислить:
|
Вычислить:
|
2 |
Сколькими способами из класса, в котором учатся 20 школьников, можно выбрать: а) двоих для участия в математической олимпиаде? б) капитана команды для математических соревнований и его заместителя? |
В классе 27 учеников, из которых нужно выбрать троих. Сколькими способами это можно сделать, если: а) 1 ученик должен решить задачу, 2 — сходить за мелом, 3 — пойти дежурить в столовую; б) им следует спеть хором? |
3 |
Сколько существует автомобильных номеров состоящих из трех цифр и трех букв? |
В чемпионате участвует 12 команд. Сколькими различными способами могут быть распределены три различные медали? |
4 |
11 футболистов строятся перед началом матча. 1-м — обязательно капитан, 2-м — обязательно вратарь, а остальные — случайным образом. Сколько существует способов построения? |
Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр? |
5 |
Запишите бином Ньютона 5степни |
Запишите бином Ньютона 6степни |
