
- •Дослідження впливу фазового складу на твердість наплавленого шару
- •Матеріали, прилади, довідкове і програмне забезпечення роботи
- •Падаючий промінь, 2 – відбитий промінь
- •1.2.Дифракційний спектр (дифрактограма) однофазного зразку
- •Підготовка зразків для дослідження на дифрактометрі
- •Звіт по роботі
- •Контрольні запитання для самоперевірки і контролю підготовленості до лабораторної роботи
- •Варіанти завдань до роботи №1
- •Вивчення впливу лазерної обробки деталей на залишкові напруження
- •Загальні та теоретичні відомості
- •Підготовка зразків для рентгенівських зйомок
- •Порядок проведення роботи
- •Звіт по роботі
- •Контрольні запитання для самоперевірки і контролю підготовленості до лабораторної роботи
- •Варіанти індівідуальних завданнь до роботи №2
- •Визначення хімічного складу та дослідження розподілу елементів методом мас – спектроскопии вторинних іонів
- •Матеріали, прилади, довідкове і програмне забезпечення роботи
- •2.Загальні та теоретичні відомості
- •4.Порядок проведення роботи
- •Контрольні запитання для самоперевірки і контролю підготовленості до лабораторної роботи
- •Варіанти індивідуальних завданнь до роботи№3
- •Дослідження розподілу елементів методом рентгеноспектрального мікроаналізу
- •1.Загальні та теоретичні відомості
- •6.Порядок проведення роботи
- •Контрольні запитання для самоперевірки і контролю підготовленості до лабораторної роботи
- •Варіанти завданнь до лабораторної роботи №5
- •Дослідження впливу величини зерна феріту на механічні властивості відпаленої сталі
- •Прилади, матеріали, довідкове і програмне забезпечення роботи
- •Теоретичні відомості
- •Звіт по роботі
- •Варіанти завданнь до лабораторної роботи №6
- •Вивчення методик виготовлення зразків для мікроструктурного та мікродюрометричного аналізу
- •Визначення мікротвердості фазових складових сплавів
- •Призначення
- •2. Порядок роботи
- •2.1. Підготовка до роботи
Варіанти завдань до роботи №1
Зразки наплавлялись на лазері DY 044 при швидкості 10мм/с
Щільність потужності (р) вказана під складом присадкового порошку
Wp=(0,5…5,0)105 Вт/см2
№ 1.
Присадковий порошок Fe (основа) – Cr – B- C- Si
Р=0,8•105Вт/см2

Штрих- діаграма повна
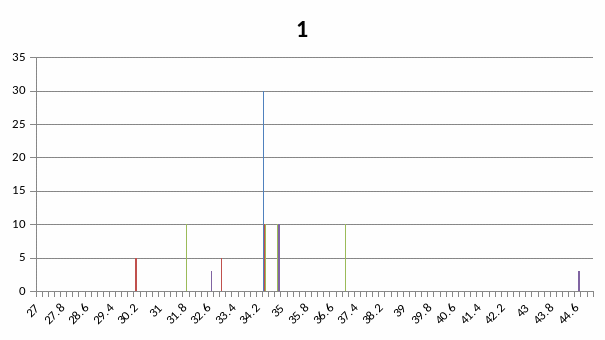
Малокутова частина дифрактограми
№2
Присадковий порошок Ni (основа) – Cr – B – C –Si
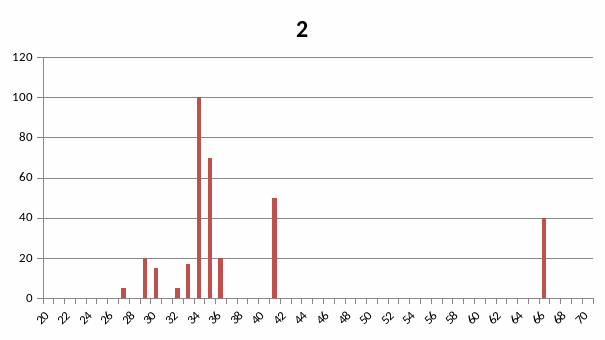
Штрих- діаграма повна

Малокутова частина штрих - діаграми
№3
Присадковий порошок Ni (основа) – Cr – B – C –Si
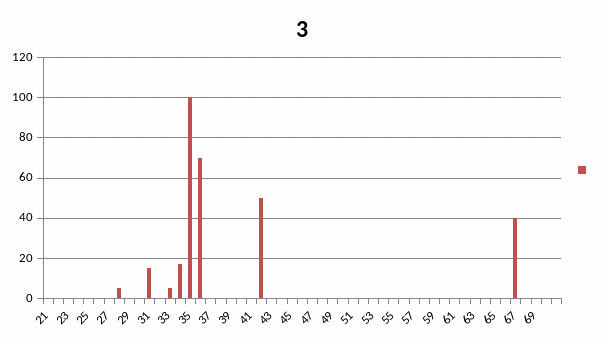
Штрих- діаграма повна
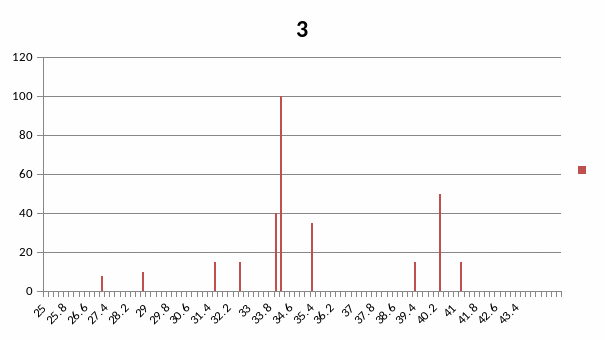
Малокутова частина штрих – діаграми
Варіант 4
Присадковий порошок Ni (основа) – Cr – B – C –Si

Штрих- діаграма повна
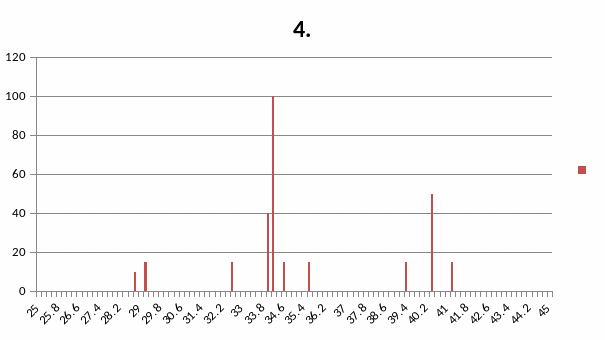
Малокутова частина штрих – діаграми
Варіант5
Присадковий порошок Ni (основа) – Cr – B – C –Si
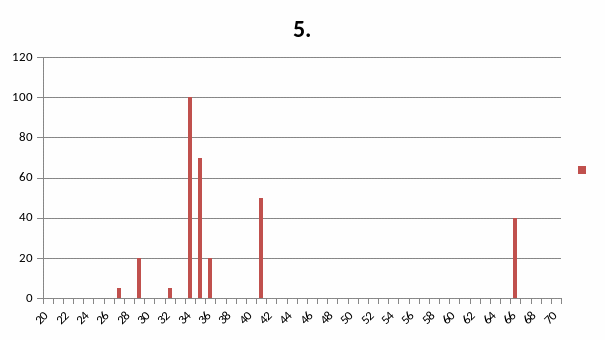
Штрих- діаграма повна

Малокутова частина штрих – діаграми
Варіант 6
Присадковий порошок Fe (основа) - Cr – B- C- Si
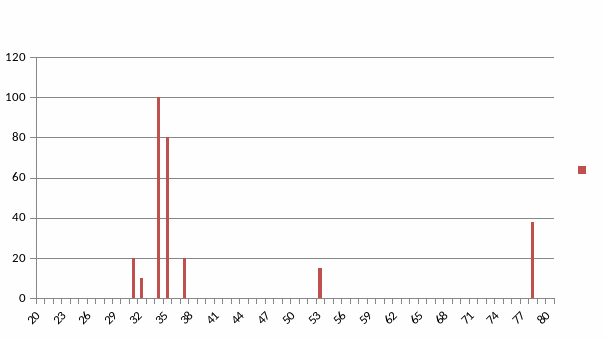
Штрих- діаграма повна
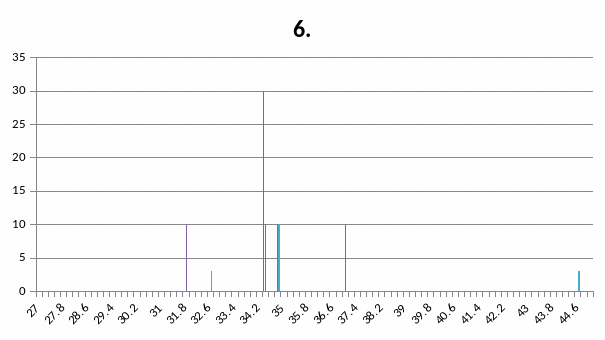
Малокутова частина штрих – діаграми
Варіант 7
Присадковий порошок Fe (основа) - Cr – B- C- Si

Штрих- діаграма повна
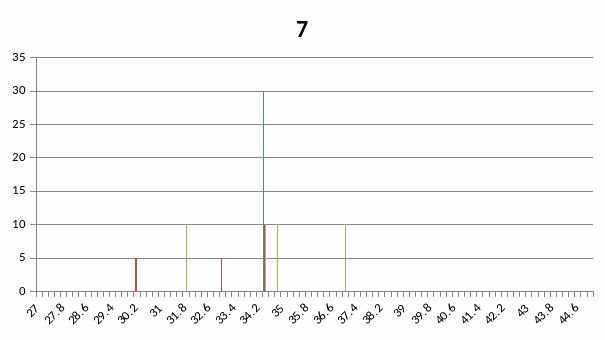
Малокутова частина штрих – діаграми
Варіант 8.
Присадковий порошок Fe (основа) - Cr – B- C- Si
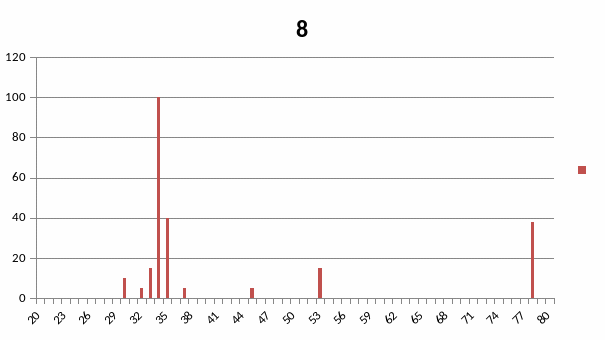
Штрих- діаграма повна
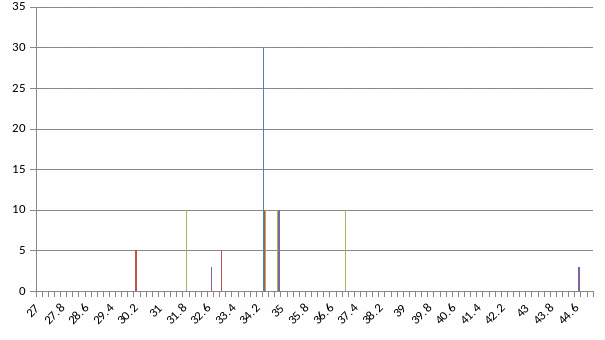
Малокутова частина дифрактограми
Варіант 9
Присадковий порошок Ni (основа) – Cr – B – C –Si

Штрих- діаграма повна

Малокутова частина дифрактограми
Варіант 10
Присадковий порошок Fe (основа) - Cr – B- C- Si

Штрих- діаграма повна
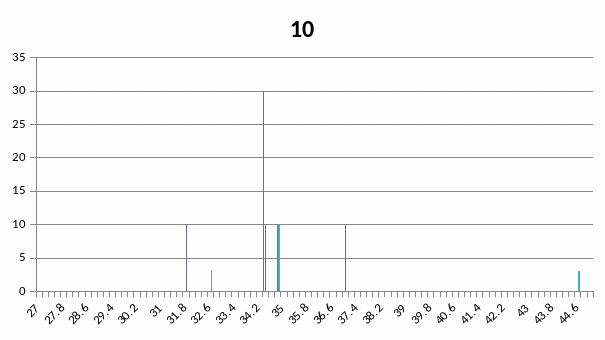
Малокутова частина дифрактограми
Лабораторна робота 2
Вивчення впливу лазерної обробки деталей на залишкові напруження
Мета
роботи.
Оволодіти методикою вимірювання
залишкових напружень рентгенівським
 - методом. Навчитися аналізувати механізми
виникнення залишкових напружень та їх
вплив на механічні властивості деталей.
- методом. Навчитися аналізувати механізми
виникнення залишкових напружень та їх
вплив на механічні властивості деталей.
Матеріали, прилади, довідкове і програмне забезпечення роботи
1. Зразки оброблені лазерним випромінюванням (гартування, легування, наплавлення)
2. Рентгенівський дифрактометр ДРОН – 2,0 (розглядається лише принципова будова)
електроно –обчислювальний пристрій
блок автоматичного керування
стійка з гоніометром та рентгенівською трубкою
високовольтне джерело живлення рентгенівської трубки
пристрій виведення інформації
3. Програма Microsoft Excel
4.Додаток1. Довжини хвиль рентгенівського випромінювання рентгенівських
трубок
Загальні та теоретичні відомості
Залишковими звуть напруження які існують в деталі або конструкції при відсутності зовнішніх силових, теплових та інших дій. Залишкові напруження (ЗН) підкорюються закону Гука та врівноважуються в усьому об‘єму зразку (або в більший його частині). Використовують і інші назви ЗН: попередні, внутрішні, напруження першого роду, технологічні напруження. Для більшої визначеності ЗН звуть по назві процесу, який проводить до їх появи – зварювальні напруження, ливарні, гартувальні напруження та ін. ЗН суттєво, а іноді вирішальне, впливають на експлуатаційні характеристики деталей машин та конструкцій.
Вплив однорідних пружних напружень на вигляд рентгенівської дифрактограми.
Розглянемо полікристалічний зразок, який пружно деформований розтягувальною силою Р (рис1.)

Рис.1. Схема пружно розтягнутого зразку.
Згідно з законом Гука відносна повздовжня деформація дорівнює
 =
ΔL/L0
= σ/E,
(1)
=
ΔL/L0
= σ/E,
(1)
де Е – модуль Юнга.
Відносна поперечна деформація дорівнює
 =
- µσ/Е,
(2)
=
- µσ/Е,
(2)
де µ - коефіцієнт Пуассона.
Деформація всього зразку спричиняє зміну розмірів кожного зерна. Це відбувається за рахунок зміни міжплощинних відстань кристалічної гратки. Причому для зерен, в яких нормалі до атомних площин паралельні Р (на рис.1 позначені як d1) повинно виконуватися рівняння
Δd1/d1 = (3)
Для зерен в яких нормалі до атомних площин перпендикулярні Р ( на рис.16 позначені як d2) виконується рівняння
(d – d0) /d0 =Δd2/d2 = (4)
де d0 - міжплощинна відстань в зразку у відсутності напружень ( в еталоні), d – міжплощинна відстань у деформованому зразку.
З формули Вульфа – Брегга (1) виходить, що зміна міжплощинних відстаней приводить до зміни кута відбиття θHKL відповідних атомних площин. Тобто наявність в зразку напружень приводить до зміщення (Δθ HKL ) дифракційних максимумів на дифрактограмі відносно ненапруженого зразка. Можна показати, що
Δθ
= σ
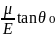 (5)
(5)
Тобто поява напружень зміщує положення дифракційного максимуму відносно θ0, а саме додаткові напруження (розтягуючи) збільшують θ, від‘ємні зменшують θ.
1.2.Теоретичні основи - метода
Напружений стан з одновісними залишковими напруженнями реалізується дуже рідко, як правило, виникає об’ємно напружений стан, який характеризується трьома головними компонентами тензору напружень σ1, σ2, σ3. Визначимо якими співвідношеннями зв’язані компоненти тензору напружень зі зміщенням дифракційних максимумів. Попердньо уведемо наступне обґрунтоване спрощення. Хаотичність орієнтації кристалів у більшості матеріалів з яких виготовляються деталі дозволяють вважати, що анізотропія пружних властивостей не проявляється. В такому разі виконується закон Гука, а деформацію тіла зручно описувати еліпсоїдом деформацій (рис.2). Еліпсоїд деформацій це поверхня в яку перейде сфера одиничного радіусу під дією ЗН.

Рис. 2. Еліпсоїд деформацій
Рівняння еліпсоїду деформацій у сферичних координатах має вигляд
εψ,φ = ε1α²1 + ε²2α²2 + ε3α²3 (6)
де - εψ,φ – деформація у направленні, що задана кутами ψ та φ; ε1, ε2 та ε3 – головні нормальні деформації: α1, α2, α3 - напрямні косинуси напрямку вимірювання деформації відносно головних осей. З рис.2 видно, що
α1
=
 α2
=
α2
=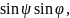 α3
=
α3
=
 (7)
(7)
Підставивши (7) у (6) одержимо
εψ,φ
= (ε1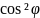 + ε2
+ ε2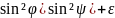 3
3 (8)
(8)
Згідно з узагальненим законом Гука зв'язок між деформаціями та напруженнями такий
ε1 = [σ1 - µ(σ2 + σ3)]/Е
ε2 = [σ2 - µ(σ1 + σ3)]/E
ε3 = [σ3 - µ(σ1 + σ2)]/E
Підставивши
ці рівняння в (8), з урахуванням відомого
співвідношення
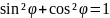 та позначив
та позначив
σψ=90°,φ
= σφ
= σ1 2
2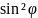 (9)
(9)
отримаємо
εψ,φ
=
 ( σφ
– σ3)
( σφ
– σ3)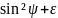 3
(10)
3
(10)
В (9) σφ – компонента нормальних напружень, що знаходиться в головній площині (рис.3)

Рис.3. Схема вимірювання деформації εψ,φ
N – нормаль до поверхні зразка,
σ1, σ2, ε1, ε2, ε3 – головні напруження та деформації
ѕ0, ѕ1 – первинний та відбитий промінь
З
умов рівноваги виходить, що на поверхні
зразку σ3
= 0 ( на поверхню не діють зовнішні сили).
Відомо, що товщина шару, що формує
дифракційний максимум не перевищує
 .
Тому можна вважати, що в рівнянні (10) σ3
= 0 ( лише при дуже високому градієнті
напружень це припущення не зовсім
справедливе ). Ця обставина дозволила
стверджувати, що рентгенівським методом
аналізується двовісний напружений стан
тоді рівняння (10) приймає форму
.
Тому можна вважати, що в рівнянні (10) σ3
= 0 ( лише при дуже високому градієнті
напружень це припущення не зовсім
справедливе ). Ця обставина дозволила
стверджувати, що рентгенівським методом
аналізується двовісний напружений стан
тоді рівняння (10) приймає форму
εψ,φ
=
 φ
+ ε3
(11)
φ
+ ε3
(11)
Рівняння
(11) - основне в
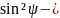 методі,
його особливістю є лінійна залежність
деформації від параметру
,
що й дало назву методу.
методі,
його особливістю є лінійна залежність
деформації від параметру
,
що й дало назву методу.
Виразимо відносні деформації в (11) через міжплощинні відстані
εψ,ϕ
=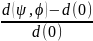 (12)
(12)
ε3
= ε┴=
 = -
= -
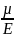 (σ1
+
σ2
)
(13)
(σ1
+
σ2
)
(13)
де d(0) - міжплощинні відстані зразка в якому відсутні залишкові напруження.
Визначаючи величини міжплощинних відстаней з формули Вульфа – Брегга маємо
εψ,ϕ=
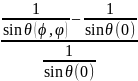 =
=
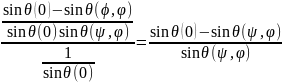 (14)
(14)
ε3
=
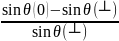 (15)
(15)
У більшості практично важливих випадків величина d(0) невідома і рівняння (11) перетворюють у приблизну формулу
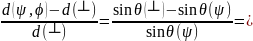 φ
(16)
φ
(16)
Всі розрахунки у роботі проводяться по співвідношенню (16).
Визначення головних напружень.
Важливе знання саме головних напружень σ1 та σ2. Для їх визначення з формули (16) треба знати їх орієнтацію у деталі. Направлення σ1 та σ2 визначаються або симетрією деталі або технологією обробки. Так якщо оброблена поверхня має циліндричну форму, то, як правило, σ1= σz σ2 = στ. При обробці пласкої поверхні безперервним лазерним випромінюванням (рис.4) головні напруження орієнтовані вздовж та перпендикулярно доріжці. Якщо зона одночасної обробки поверхні має кругову симетрію, в шарі повинні формуватися площинні ізотропні напруження, тобто σφ= σ1= σ2 = σі. В цьому випадку зразок може мати довільну орієнтацію відносно променя. Студент вказує оператору рентгенівської установки направлення головних напружень. Оператор належним чином орієнтує зразок (рис.4) і видає значення θ для двох рівнянь
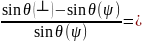
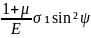 (17)
(17)
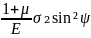 (18)
(18)

Рис.4. Положення зразка відносно рентгенівського
променя при визначенні στ
у вигляді таблиці
-
ѱ
Θ1
Θ2
0
26,6
39,2
50,8
78,04
78,06
78,1
78,12
78,04
78,02
78,0
77,96
По даним таблиці будуються два графіка.
1.4.Одержання - графіка в Excel і розрахунок напружень
Розрахуємо величину напружень в сплаві на базі α - Fe по даним зйомки віддзеркалення 211 у CrKα випромінюванні. Первинні дані мають такі значення
ψ |
θ |
0 |
78,12 |
26,6 |
78,13 |
39,2 |
78,15 |
50,8 |
78,16 |
Після розрахунку маємо таблицю для будування – графіку:
-
ε(ψ)=
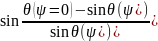
0
0
0,2
-0,00004
0,4
-0,0001
0,6
-0,00014
Після введення цих даних в таблицю Excel та виконання послідовності дій, що показані на скріншотах









маємо - графік та його рівняння (рис.28 )
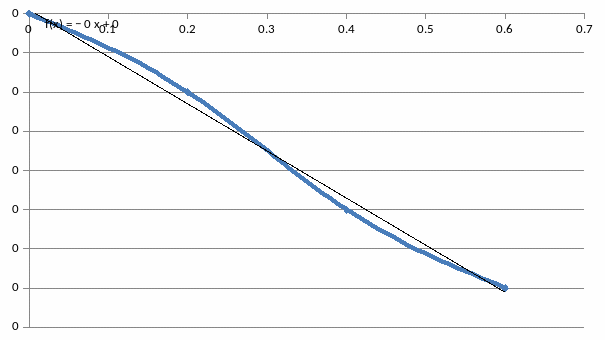
Рис.5. - графік сплаву на базі α - Fe.
З
рівняння прямої маємо
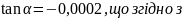 формулой (12)
при Е211
= 21Е4МПа, μ211=0,28
дає σφ=
- 50МПа.
формулой (12)
при Е211
= 21Е4МПа, μ211=0,28
дає σφ=
- 50МПа.
