1.Производная тригонометрических функций.

1)(sinx)

2)

3)

4)

2.Непрерывность функций в точке на множестве.

Функция f(x) называется непрерывной в точку x= если предел функции и её значение в этой точке равны, то есть f(x)=f(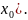

Если функция f(x) непрерывна в каждой точке множества, то он называется непрерывной функцией на данном множестве.

БИЛЕТ № 12.

1.Производная сложной функции.

Общий вид функции: y=f(g(x))

Если функция y=f(u) имеет производную в точке а другая функция u=g(x) имеет производную в точке , причём то существует производная для сложной функции y=f(g(x)) в точке , которая вычисляется по формуле:

2.Уравнение sinx=a. Частные случаи корней уравнения sinx=a.

sinx=a x=(

Частные случаи:

sinx=1

x=

sinx=-1

x=

sinx=0

x=

БИЛЕТ № 13.

1.Определение возрастающей и убывающей функции на множестве х. Примеры.

Возрастающая (убывающая) функция на Х – если на множестве Х функция y=f(x) для любых чисел выполняется неравенство f( f( )

Когда функция убывает, то х-увеличивается. у-уменьшается. При возрастании х,у - увеличиваются

Пример:

2.Уравнения tgx=a, ctgx=a

БИЛЕТ № 14.

1.Определеия точек максимума и минимума, экстремума функции.

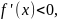Если функция f(x) в точке непрерывна, а на интервале (a; ) на интервале( то точка является точкой максимума.

Если функция f(x) в точке непрерывна, а на интервале (a; ) на интервале( то точка является точкой минимума

Точки минимума и максимума в общем случаи называются точками экстремума.

2.Формулы для вычисления приближённых вычислений.

БИЛЕТ № 15.

1.Определение обратной функции. Найти функции, обратные функциям y=2x-3 и y=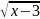

Пусть обратимая функция y=f(x) определена на множестве Х и Е (f)=Y. Поставим в соответствие каждому у из У то единственное значение х, при котором f(x)=y (единственный корень уравнения f(x)=y относительно х). Тогда получим Функцию с областью определения У и множеством значений Х. Эта функция называется обратно по отношению к функции y= f(x), х

1)у=2х-3

х=

у=

у+3=2х

х=

2)у=

х= +3

у=