БИЛЕТ № 1.

1.Определение функции, области определения и множества значений.

Функция – закономерность, при котором каждому значению х из множества Х соответствует единственное значение у из множества У.

Область определения D(f(x)) - множество значений независимой переменной, при которых функцию f(x) принимает вполне определённые значения.

Множество значений функции Е(f(x)) – значение функции, соответствующие каждому значению независимой переменной и области определения.

Пример:

a) y=2 b)y= c)y=

D(f)=R 2x-1

x≠±3 x

D(f)=(-∞;−3) (−3;3) (3;+∞)

x

2.Функция y=cosx, её свойства и график.

1) D(y)=R

2) E(y)= [-1;1]

3) T=2 ; cos(x+2

4) f(-x)=cos(-x)=cosx (функция чётная)

5) убывает [2

возрастает [- ],

БИЛЕТ № 2.

1.Способы заданий функции.

-Аналитический способ: заключается в том, что функция задаётся формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.

-Графический способ: при графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (х;у)

-Табличный способ: при этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие числу У.

2.Функция y=cosx, её свойства и график.

1) D(y)=R

2) E(y)= [-1;1]

3) T=2 ; sin(x+2

4) f(-x)=sin(-x)=-sinx (функция нечётгая)

5) Возрастает [

Убывает [

БИЛЕТ № 3.

1.Определение чётной, нечётной функции, функции общего вида.

-Чётная функция: f(-x)=f(x)

Пример: 1) f(x)=сosx

f(-x)=cos(-x)=cosx

2) f(x)=

f(-x)=

График симметричен относительно оси Оу.

-Нечётная функция: f(-x)=-f(x)

Пример: 1) f(x)=sinx

f(-x)=sin(-x)= -sinx

2) f(x)=

f(-x)=(-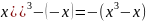

Симметричен относительно начала координат

-Функция общего вида:

Пример: 1) f(x)=

f(-x)=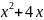

2.Основные тригонометрические тождества. Доказательства одного из них.

1)

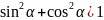
2)

3)

4)1+

5)1+

6)

Доказательство:

По теореме Пифагора

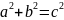
. Разделим две части неравенства на .

.

По определению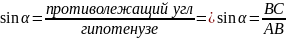

Подставим

БИЛЕТ № 4

1.Определение периодической функции, примеры периодических функций, иллюстрация на графике. Найти наименьший положительный период функции y=sin3x

Если найдётся такое число Т , что для любых х из области определения у= f(x) выполняется равенство f(x+Т)= f(x), то это периодическая функция.

Пример: y=sinx

sin (x+2

T=

y=sin3x, у sin T=

T=

2.Формулы суммы разности косинусов (синусов). Доказательство одной из формул.

a)

b)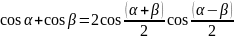

Доказательство:

Разложим ;

sin =sin

Подставим:

sin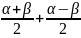 =sin( )+sin( )=sin

=

БИЛЕТ № 5.