1.3. Средняя форма общих индексов

Для определения общих индексов цен и физического объема продукции в агрегатной форме необходимы данные о количестве отдельных видов продукции в натуральных измерителях. Но часто учет объемов производства ведется непосредственно в стоимостном (денежном) выражении, что делает неприменимой агрегатную форму общих индексов. В таких случаях для определения сводных обобщающих показателей изменения цен или физического объема продукции используется средняя арифметическая или средняя гармоническая форма общих индексов. Выбор той или иной формы среднего индекса определяется прежде всего исходными данными, которые имеют в наличии при решении конкретных задач.

Средние индексы Ip или Iq вычисляются на основе соответствующих индивидуальных индексов i_p или i_q путем осреднения их и выбором таких весовых коэффициентов в такой форме, чтобы расчетная формула каждого среднего индекса формально совпадала с формулой соответствующего агрегатного индекса.

Так, при наличии данных только о стоимости продукции отчетного периода p₁ q₁ в ценах этого же периода и наличии данных по i_p расчет индекса цен Ip по формуле Пааше невозможен. В этом случае применяется формула гармонической средней индивидуальных индексов цен i_p:

Ip = 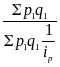. (1.11)

Нетрудно видеть, что преобразование формулы Пааше (1) выполняется формальной заменой в выражении знаменателя p₀ q₁ величины p₀ с помощью индивидуального индекса i_p = p₁/p₀ на p₁: p₀ = p₁/ i_p.

Если в наличии имеются только данные о стоимости продукции базисного периода в базисных ценах p₀ q₀ индекс цен Ip нельзя рассчитать по формуле Ласпейреса (2). Это можно сделать только по арифметической средней индивидуальных индексов цен:

Ip = . (1.12)

Аналогично можно показать, что эта формула преобразуется в выражение индекса Ласпейреса.

Таблица 1.2

Расчет индекса Iq в среднегармонической форме

Вид про-	Продукция текущего	Рост объема про- дукции по отно-	Расчетные графы
дук-ции	периода, тыс.руб	шению к базисному периоду, %
А	165,20	20	1,20	137,67
Б	123,40	12	1,12	110,18
В	320,00	-5	0,95	336,84
Г	276,40	0	1,00	276,40
Итого	885,00			861,09

Iq = 885,00 /861,09 = 0,973 - индекс физического объема продукции в форме Пааше.

pq(q) = 885,00 - 861,09 = - 23,91 тыс. руб - изменение стоимости в текущем периоде за счет изменения физического объема продукции.

Подобные формулы нетрудно получить и для расчета индексов физического объема продукции по средней арифметической и средней гармонической индивидуальных индексов физических объемов i_q.

Важной отличительной особенностью такой формы индексов является то, что в качестве весов усредняемых индивидуальных индексов выступают реальные экономические категории: p₁ q₁ и p₀ q₀ - фактическая стоимость продукции текущего (отчетного) и базисного периодов.