3.2.Двумерный спектр морского волнения

Совместим морскую поверхность в спокойном состоянии (полный штиль) с плоскостью XOY декартовой системы координат. Тогда высоты возвышения волн будут проецироваться на ось Z. Каждая точка на морской поверхности будет являться функцией пространственных координат x и y. Поскольку волны, образующие случайное поле морского волнения, имеют вполне определенные скорости распространения, каждая точка морской поверхности зависит от временной координаты t. Таким образом, поверхность моря есть трехмерный случайный динамический процесс z(x,y,t) с нулевым средним значением.

В спектральной теории волновых процессов, к которым относится трехмерное поле морского волнения, в качестве базисных функций рассматриваются также трехмерные волны с синусоидальным профилем (сечение в плоскости XOZилиYOZ). При этом рассматриваются два основных типа волн: с бесконечным плоским фронтом и с радиальным фронтом. В общем случае, даже при пространственно распределенном внешнем воздействии (типа ветра у поверхности моря) его можно представить как совокупность элементарных сосредоточенных воздействий, каждое из которых порождает волны с радиальным фронтом (принцип Гюйгенса - Френеля). В этом смысле волны с радиальным фронтом являются более естественными базисными функциями, однако они не позволяют в простой форме связать энергию воздействия с полной энергией морского волнения, приходящуюся на единицу площади, поскольку необходимо учитывать естественное ослабление радиальных волн за счет рассеяния энергии каждой волны в пространстве. Поэтому на практике большее распространение получили базисные функции в виде идеализированных синусоидальных волн с бесконечными плоскими фронтами.

Каждая i-я волна с плоским фронтом из множества волн, образующих случайный волновой рельеф, характеризуется волновым числом К_i и направлением распространения _i относительно оси Х. Эту волну можно рассматривать как спектральную составляющую морского волнения. Для волнового числа справедливо соотношение:

, (3.4)

где _i - длина волны спектральной составляющей морского волнения.

В соответствии с соотношением (3.3) морские волны разной длины обладают дисперсией, другими словами, пакеты морских волн со временем “рассыпаются” из-за различной фазовой скорости распространения отдельных спектральных составляющих.

Рис. 3.3.

Для конкретной синусоидальной морской волны с фиксированным волновым числом К_i, распространяющейся в направлении _j (рис. 3.3), справедливо представление обусловленной ею высоты возвышения поверхности моря z_ij в виде составляющих проекций по осям X и Y:

, (3.5)

где A_ij и _ij - соответственно амплитуда и начальная фаза данной компоненты пространственно-временного спектра морского волнения, а =2/Т - круговая частота колебаний морской волны с периодом Т. Общее поле морского волнения, представляющего собой совокупность отдельных разноориентированных синусоидальных волн с плоскими фронтами, может быть записано как результат суперпозиции отдельных волн с волновыми числами К_i и направлениями _j, поэтому результирующее возвышение представимо в декартовых координатах в виде двойных сумм выражения (3.5) по всем возможным К_i и _j проекций каждой волны на оси Х и Y:

(3.6)

ЭнергияЕ_ij, содержащаяся в отдельной спектральной составляющей морского волнения, определяется ее амплитудой A_ij и не зависит от фазовых соотношений, поэтому с точностью до постоянного множителя можно записать:

, (3.7)

где k - коэффициент пропорциональности, определяемый плотностью морской воды . Для волн, образующих случайное поле волнения, описываемое выражением (3.6), справедливо соотношение: 2k=g.

Двухмерный энергетический спектр морского волнения в полярных координатах S(K,) можно определить как характеристику распределения энергии морских волн по волновым числам К_i и направлениям распространения _j. Тогда энергия, сосредоточенная в бесконечно узкой полосе значений волновых чисел К и направлений распространения , может быть представлена в виде

. (3.8)

Из сопоставления двух выражений (3.7) и (3.8) можно заключить, что амплитуда элементарной спектральной составляющей может быть определена из двухмерного спектра морского волнения:

. (3.9)

Для описания двухмерного спектра морского волнения в декартовых координатах введем волновые числа по осям координат Х и Y (рис. 3.1):

, (3.10)

которые являются проекциями исходного волнового числа К на оси Х и Y при направлении распространения . Из (3.10) очевидно, что

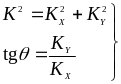(3.11)

Переход от спектра в координатах {K,} к спектру в координатах {K_X, K_Y} осуществляется на основе следующего равенства:

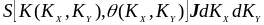, (3.12)

где якобиан преобразования J имеет вид:

. (3.13)

Подставив в (3.12) и (3.13) функциональные зависимости, полученные на основании выражений (3.10) и (3.11), и выполнив несложные преобразования, получим J=K^-1, откуда

. (3.14)

В качестве примера на рис. 3.4 представлена диаграмма сечений равного уровня типичного двумерного спектра морского волнения S(K_X,K_Y) вида (3.14) в декартовых координатах.

Во многих практических задачах вместо волнового числа К удобнее использовать круговую частоту , связанную с волновым числом соотношением

. (3.15)

В этом случае двухмерный спектр морского волнения записывается в координатах {, } как

, (3.16)

где якобиан преобразования c учетом (3.15) имеет вид:

. (3.17)

Рис.3.4.